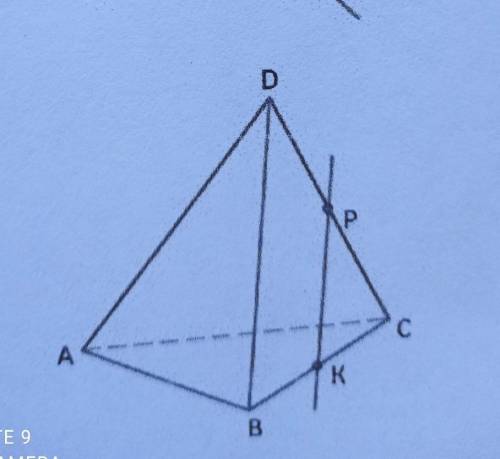
В тетраэдре DABC BK=KC,DP=PC.Плоскости какой грани параллельна прямой PK.ответ Обоснуйте​

Чтобы решить данную задачу, давайте разберемся с основными понятиями. В данном случае у нас есть тетраэдр DABC, а также точки K и P. Нам дано, что отрезок BK равен отрезку KC (BK = KC), а также отрезок DP равен отрезку PC (DP = PC). Также нам известно, что нужно найти плоскость, которая параллельна прямой PK. Для начала, давайте разберемся с определениями и свойствами тетраэдра и его граней. Тетраэдр - это многогранник, который состоит из четырех граней. Каждая грань тетраэдра - это треугольник. Грани тетраэдра обычно обозначаются по первым буквам названий вершин. В данном случае, у нас есть графическое изображение тетраэдра DABC. Теперь давайте перейдем к решению задачи. Мы хотим найти плоскость, которая параллельна прямой PK. Чтобы найти такую плоскость, мы можем использовать свойство параллельности прямой и плоскости. Если прямая параллельна одной из граней тетраэдра, то плоскость этой грани также будет параллельна этой прямой. Для нашей задачи, давайте посмотрим, какая грань тетраэдра DABC параллельна прямой PK. Мы знаем, что отрезок BK равен отрезку KC (BK = KC). Одно из свойств параллельных прямых гласит, что если прямая пересекает две параллельные прямые, то отношение отрезков, которые она образует, будет равно. В нашем случае, прямая PK пересекает прямую BC, и точка K является точкой пересечения. Таким образом, отношение отрезка BK к отрезку KC будет равно отношению отрезка BP к отрезку PC. Мы также знаем, что отрезок DP равен отрезку PC (DP = PC). Теперь давайте сравним эти два отношения. Если мы заметим, что отношение отрезка BP к отрезку PC также равно единице (BP/PC = 1), то это означает, что точка P расположена на середине отрезка BC. Если точка P находится на середине отрезка BC, то это означает, что плоскость грани DBC параллельна прямой PK. Таким образом, ответ на задачу: плоскость грани DBC параллельна прямой PK. Мы обосновали свой ответ, используя свойства параллельных прямых и отношение отрезков.