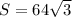В равнобедренном треугольнике высота равна 8 см, а угол при основании равен 30°. Найдите площадь этого треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Task 1. Read and find the word that matches this definition: From the...
2 - Выберите правильную неравенства...
2 - Найдите значение выражения (- 1/4+1/5)-(-0,1)...
1 - 5разрядтың 3бірлігі.4разрядтың9бірлігі.1разрядтың5бірлігі...
2 - четвёрты биноминальный коэффициент в разложении (х+у)^12 равен р . Укажити...
2 - Мәтінді оқы. Конспект жаз.Внимательно прочитайте текст и напишите конспект...
1 - 12жане 60 снадарынын еуоб жане екое комектесиниздерги...
2 - 5.Любые изменения, которые происходят в природе, называются явлениями....
2 - 63-бет 2-тапсырма. Сұрақтарға жауап бер (ответь на вопросы)...
2 - СОЧ 8 КЛАСС 4. Определите относительную молекулярную массу веществ:Mr(Caso4)=Mr...
1
ответ: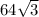
Объяснение: насколько я понял это не по тригонометрии, так что решение без нее.
в прямоугольном треугольнике напротив угла 30° находится катет, который равен половине гипотенузы.
тем катетом в данном случае является высота, а гипотенузой боковая сторона. Значит длина боковой стороны - 16 см. По теореме Пифагора находим основание(основание это - x):
далее по формуле площади треуголника находим ее: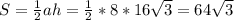
ответ: