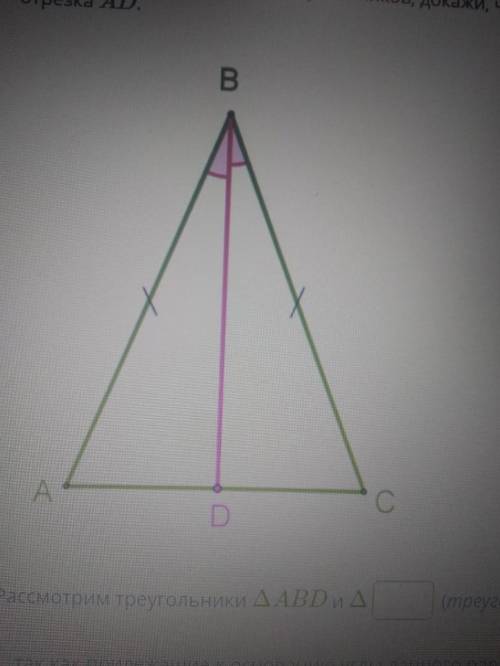
В равнобедренном треугольнике с длиной основания 8 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD. (картинка ниже)

Рассмотрим треугольники ΔABD и Δ...(треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡... ;

2. так как проведена биссектриса, то ∡... = ∡ CBD;

3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — ...

По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.

AD=...см.

9uh9ev2    2   25.12.2020 19:03    6