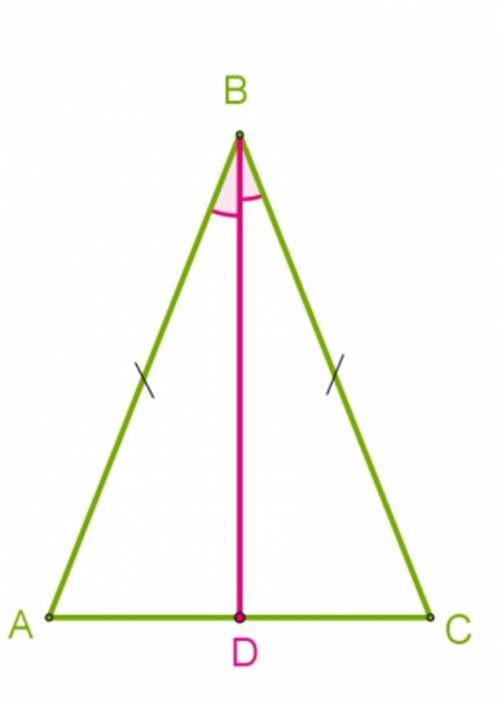
В равнобедренном треугольнике с длиной основания 49 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.
Рассмотрим треугольники ΔABD и Δ
(треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡
;

2. так как проведена биссектриса, то ∡
= ∡ CBD;

3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC —
.По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.

AD=
см.

marinka0810    3   07.11.2021 05:40    12