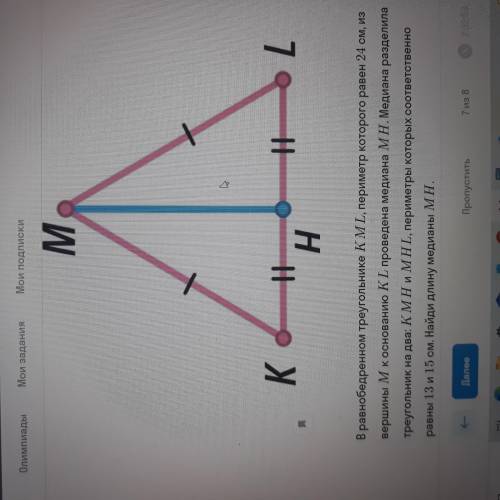
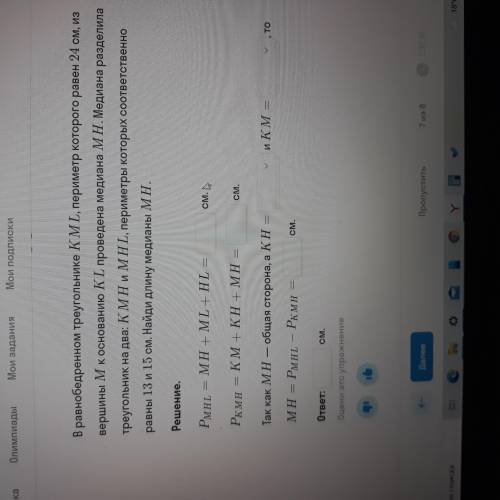
В равнобедренном треугольнике КМL, периметр которого равен 24 см, из вершины М к основанию КL проведена медиана МН. Медиана разделила треугольник на 2: KMH и МНL, периметры которых соответственно равны 13 и 15 см. Найди длину медианы МН. (Решение запишите, как на фото)
Другие вопросы по теме Геометрия
Популярные вопросы
- Дано m(SO4)=140г найти V(SO3) n(SO3) N(SO3)...
2 - Твір з описом географичного явища або об єкта?...
2 - Свойства,кота бутерброда и мяча...
2 - 16А. Прочитайте отрывок из рассказа Телеграмма Константина Георгиевича Паустовского,...
2 - Проект на тему портрет слово язык ?...
1 - Найдите в песне Ах не одна толь...
1 - Кто шарит за казахский 4б класс...
1 - Аналіз пісні: Та, ой, ЯК крикнув же та козак Сірко, Та, ой, на своїх же,...
2 - Сколько молекул соли в 30 кг?...
1 - . Виконайте додавання та віднімання даних пар чисел: – 33, -17; 41, 16....
2
Исходя из условия задачи, у нас есть равнобедренный треугольник КМL, периметр которого равен 24 см. По свойствам равнобедренного треугольника, мы можем сказать, что стороны КМ и KL равны.
Далее, проведена медиана МН, которая разделяет треугольник на два равных по площади треугольника - KMH и MNL. Периметр KMH равен 13 см, а периметр MNL равен 15 см.
Так как периметр треугольника равен сумме длин его сторон, мы можем записать следующие уравнения:
2KM + KL = 24 (уравнение для равнобедренного треугольника)
KM + MH + KH = 13 (уравнение для треугольника KMH)
MN + NH + NL = 15 (уравнение для треугольника MNL)
Так как медиана МН является линией, которая соединяет вершину М с серединой основания KL, длина медианы МН будет равна половине длины основания KL.
Чтобы решить данную задачу, мы должны найти значения KM и KL, а затем найти половину KL для определения длины медианы МН.
1. Решим уравнение для KM и KL:
2KM + KL = 24
Так как треугольник равнобедренный, KM = KL. Мы можем заменить KM в уравнении:
2KL + KL = 24
3KL = 24
KL = 8
Таким образом, длина основания KL равна 8 см.
2. Теперь, найдем длину сторон MH и NH через периметры KMH и MNL:
KM + MH + KH = 13
KM = KL (равнобедренность треугольника)
KL + MH + KH = 13
8 + MH + KH = 13
MH + KH = 5
MN + NH + NL = 15
MN = KL (равнобедренность треугольника)
KL + NH + NL = 15
8 + NH + NL = 15
NH + NL = 7
3. Найдем длину медианы МН, используя KM и KL:
MN = KL (равнобедренность треугольника)
MH + NH = (KL + MH + NH) - KL
MH + NH = 5 - 8
MH + NH = -3
Таким образом, длина медианы МН равна половине длины основания KL, то есть МН = KL/2 = 8/2 = 4 см.
Ответ: Длина медианы МН равна 4 см.