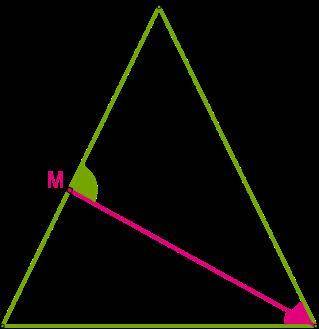
В равнобедренном треугольнике KEP проведена биссектриса PM угла P у основания KP, ∡ PME = 72°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
∡ K =
∡ P =
∡ E =
Другие вопросы по теме Геометрия
Популярные вопросы
- Хлп извиняюсь не по теме приложения, но всё же кто знает в такой...
3 - Накресліть одиничне півколо, узявши за одиничний такий відрізок,...
2 - Даю 100 ба тест а и Б ответ...
1 - Равномерное прямолинейное движение...
3 - Скажите , какой замок подойдет на шкафчик Практик LS 22. Очень...
3 - 4. Про що нам розповідають книги? Чого навчають?...
2 - Макс кол-во дам, если решите (только нормально, а не просто ответ)...
1 - картографического изображения мирового океана...
1 - Напиши Эссе, право нарушения в обществе связанно с незнанием закона...
1 - Марфемный разбор слова Взрослые...
1
1. Заметим, что у равнобедренного треугольника две равные стороны, KP и EP, так как они являются основаниями. Следовательно, углы ∡ K и ∡ E равны.
2. Так как PM является биссектрисой угла P, она делит его на два равных угла: ∡ MPK и ∡ MPE.
3. Для решения задачи нам дано значение ∡ PME, которое равно 72°.
4. Заметим, что ∡ PME является внешним углом треугольника MPE. Из свойства внешних углов треугольника, мы знаем, что он равен сумме двух внутренних углов:
∡ PME = ∡ MPK + ∡ MPE
72° = ∡ MPK + ∡ MPE
5. Так как мы знаем, что углы ∡ K и ∡ E равны, можем обозначить их как α. Тогда у нас получится следующее:
∡ MPK = α
∡ MPE = α
6. Подставляем эти значения в уравнение из предыдущего шага:
72° = α + α
7. Упрощаем уравнение:
72° = 2α
8. Решаем уравнение относительно α, деля обе части на 2:
α = 72° / 2
α = 36°
9. Таким образом, углы ∡ K и ∡ E равны 36° каждый.
10. Для определения угла ∡ P, мы можем использовать тот факт, что сумма углов в треугольнике равна 180°. Таким образом:
∡ P = 180° - 2α
∡ P = 180° - (2 * 36°)
∡ P = 180° - 72°
∡ P = 108°
Итак, для равнобедренного треугольника KEP с проведенной биссектрисой PM угла P у основания KP, углы данного треугольника имеют следующие значения:
∡ K = 36°
∡ P = 108°
∡ E = 36°