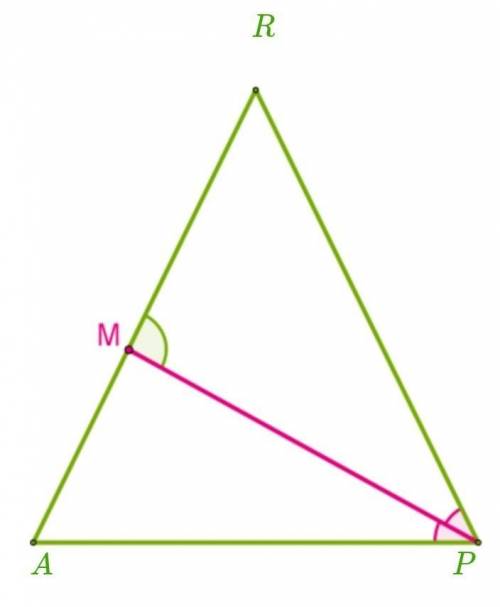
В равнобедренном треугольнике ARP проведена биссектриса PM угла P у основания AP, ∡ PMR = 72°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
∡ A = °;
∡ P = °;
∡ R = °.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1) ниже схемы видоизмените в уравнения возможных реакций: а)h2so4+? →znso4+?...
3 - Решить по рассчитать давление,которое оказывает стол, если на него действует...
1 - Два самолета летели с одинаковой скоростью первый самолет был в воздухе 4 часа...
1 - Прочитай. выпиши имена числительные измени выделенные числительные по падежам...
2 - Предложения с дополнениями со словами июль,удочка,дорога....
3 - Сестра моей подруги работает швеей. разобрать предложение по частям речи...
1 - Чему равна скорость электромагнитного поля...
3 - Как по пишется: письмо мамы ,конверт тайни , сумка почиальёна, плокаты джима...
1 - Тело движется по закону s(t) = 8 + 15t + t^2 - 1/3 t^3, где s(t) измеряется в...
2 - Всостав пояса передних конечностей земноводных входит...
2
Объяснение:
Пусть угол МРR=х, тогда угол АРR=2х.
Угол АРR=углу РАR=2х, так как у равнобедренного треугольника углы при основании равны.
Угол RMP и угол АМР-смежные. Сумма смежных углов равна 180°.
Угол АМР=180°-72°=108°
Рассмотрим треугольник АМР:
Угол АМР=108°; угол МАР=2х; угол МРА=х.
Сумма углов треугольника равна 180°
Решим с уравнения:
2х+х+108=180
2х+х=180-108
3х=72
х=72:3
х=24
Угол МРА=24°
Угол МАР=2*24°=48°
Угол РАR=углу APR=48°
Как я и говорила раньше сумма углов треугольника равна 180°.
Найдём угол при вершине АRP:
Угол ARP=180°-(48°+48°)=84°