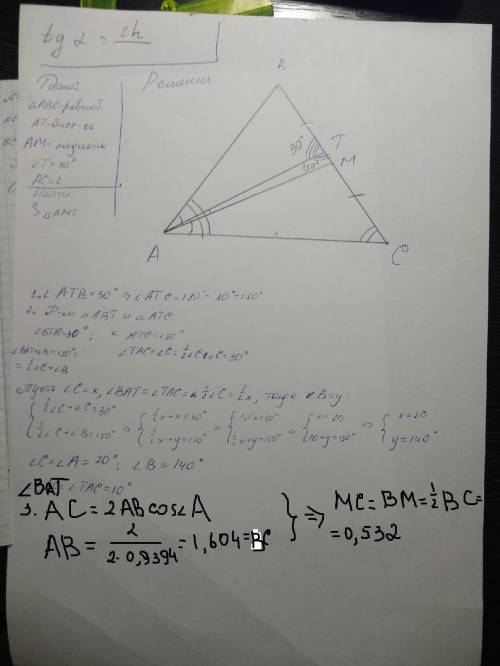
В равнобедренном треугольнике ABC с основанием АС проведены биссектриса АТ и медиана АМ. Найдите площадь треугольника АМТ, если ∠Т=30°, АС=2. Решила до этого момента. Что дальше, чтобы найти площадь АМТ?
Другие вопросы по теме Геометрия
Популярные вопросы
- Разобрать слова по составу, слова: проглотить, ,, посмотреть, осмотреть, кричать,...
3 - Какой порядок действий рекомендуется при оказании терпящему бедствие на воде?...
2 - При скрещивании растений, имеющего черные семена с белосемянным растением,...
3 - Скоромовка начинается со слов годувала гава...
2 - Определите массовую долю сахарозы в растворе, полученном растворением 2 моль...
1 - Мальчик масса которого 46 кг , прыгнул с неподвижного плота массой 1 т на берег...
2 - Какова роль женщин в наше время? (в защите отечества) если во время второй...
1 - Буквам встать так, чтобы можно прочитать слова ( при составлении слов надо...
2 - Втрапеции abcd с основаниями ad и bc угол=50.а угол с=100 найдите остальные...
1 - Решить ребус: ц ц ,ель над ней 1,гитара 2 впереди и 2 сзади,марковь над ней...
1
Первое свойство, которое нам понадобится, гласит: "В равнобедренном треугольнике биссектриса, медиана, высота, проведенные из вершины, делят основание на равные отрезки".
Дано, что треугольник ABC - равнобедренный с основанием АС. Проведены биссектриса АТ и медиана АМ, а также известно, что угол Т равен 30°, а АС равно 2.
Поскольку треугольник равнобедренный, то мы можем сказать, что отрезки АТ и МТ равны.
Для начала найдем длину отрезка МТ с помощью тригонометрических соотношений.
В треугольнике АТМ у нас известен угол Т (30°) и сторона АС (2). Мы хотим найти сторону МТ. Здесь нам может помочь тангенс угла Т:
tan(Т) = МТ / АС
tan(30°) = МТ / 2
0.577 = МТ / 2
МТ = 0.577 * 2
МТ = 1.154
Таким образом, мы нашли длину отрезка МТ.
Теперь, чтобы найти площадь треугольника АМТ, нам понадобится еще одно свойство равнобедренных треугольников. Говорится, что любая медиана треугольника делит его на два треугольника равной площади.
Зная, что отрезок МТ равен половине медианы АМ и высоты треугольника АМТ, мы можем записать формулу площади как:
P (площадь) = (МТ * h) / 2,
где h - высота треугольника.
Чтобы найти высоту треугольника, мы можем использовать формулу для нахождения высоты равнобедренного треугольника:
h = √(АС² - (МТ / 2)²),
где АС - основание треугольника.
Подставляем известные значения:
h = √(2² - (1.154 / 2)²)
h = √(4 - 0.666)
h = √3.334
h = 1.826
Теперь мы знаем длину отрезка МТ и высоту треугольника АМТ. Можем рассчитать площадь треугольника АМТ:
P = (МТ * h) / 2
P = (1.154 * 1.826) / 2
P = 2.107 / 2
P = 1.0535
Таким образом, площадь треугольника АМТ равна приблизительно 1.0535.