В равнобедренном треугольнике АBC , B E - высота, АB=BC . Найдите АB , если АC=10 √ 5 и BE=10

AB = 15

Объяснение:

Равнобедренный треугольник -  треугольник у которого две равные боковые стороны (AB = BC - ?) и основание (AC = 10√5). BE = 10 - высота.

Рассмотрим прямоугольный треугольник Δ ABE (Δ ABE = Δ BEC). Знаем катет BE = 10, второй катет AE (AE = EC) - половина стороны AC а именно: AE =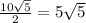 . По теореме Пифагора найдем гипотенузу с катетов, где a, b - катеты, c - гипотенуза:

AB = 15

Объяснение:

ΔABC - равнобедренный

АВ = ВС - боковые стороны

АС = 10√5 - основание

ВЕ = 10 - высота, опущенная н основание

----------------------------

АВ - ?

---------------------------

По теореме Пифагора

AB² = BE² + (0.5AC)²