В прямоугольной трапеции ABCK большая боковая равна 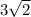
,угол K равен 45°,а высота CH делит основание AK пополам , найдите площадь трапеции
Другие вопросы по теме Геометрия
Популярные вопросы
- Кого, по вашему мнению, можно считать великими людьми последнего века римской...
1 - 1. Александр Иванович Опарин был приверженцем гипотезы о происхождении жизни:...
2 - Контрольна робота з теми різноманітність рослин варіант 1 тести...
2 - 1. Справжнє ім`я Івана Сили, який понад сто років був чемпіономЧехословаччини...
1 - Скільки клітин утворюється під час сперматогенезу з однієї вихідної клітини?...
1 - Какая форма сбережений наиболее эффективна, почему ? какая форма завершения ведет...
2 - Определить молярную концентрацию эквивалента (нормальную концентрацию) раствора...
2 - Розв яжіть запропоновані задачі. 1) Для реакції взяли алюміній гідроксид масою...
3 - Какие должности в риме занимал октавиан август после победы над республиканцами...
2 - Choose a sportsperson from any country and write about him/her using a plan...
2
ответ: 13,5 см ².
Объяснение:
Решение.
ABCК - трапеция.
Высоту трапеции h = CН находим из треугольника CHК
CM = 5√2 см. Углы при основании∠M = ∠ HCM = 45*.
Тогда СH=HК=h = (CК*√2)/2 = 3√2*√2/2=3 см.
Так как AH=HК, то AК = 2 HК = 2*3=6 см .
ВС=3 см.
S=h(a+b)/2 =3(3+6)/2 = 3*9/2=13,5 см ².