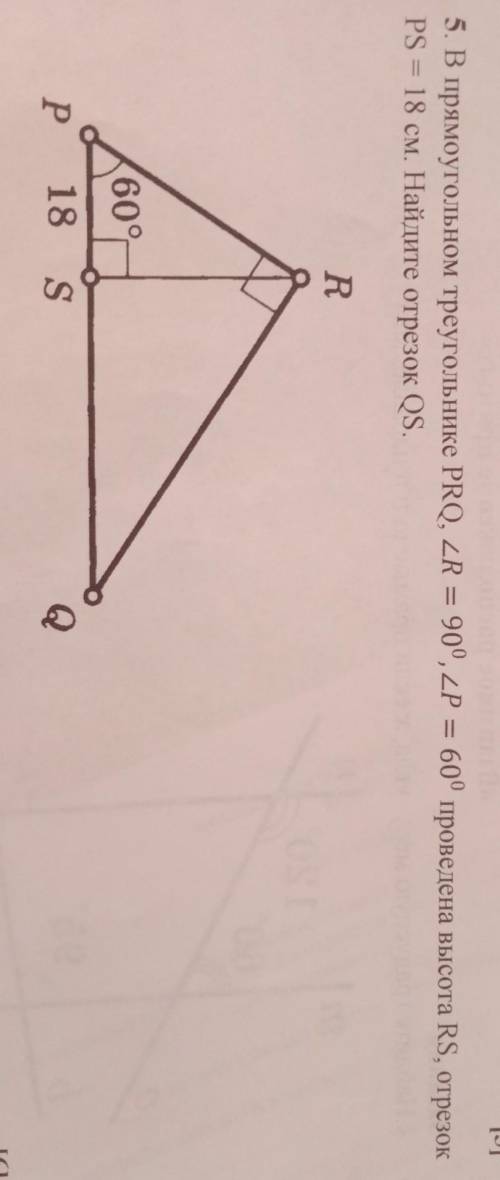
В прямоугольном треугольнике PRQ, ∠R=90°, ∠P=60° проведена высота RS, отрезок PS=18 см. Найдите отрезок ещё с этим...​

Добрый день! Давайте рассмотрим данную задачу.

Мы знаем, что треугольник PRQ является прямоугольным, то есть угол R равен 90 градусов.
Также в задаче указано, что угол P равен 60 градусов.

Высота RS проведена из вершины P и перпендикулярна стороне PR.

Теперь, чтобы решить эту задачу, нам нужно найти отрезок QR.

Для начала, рассмотрим треугольник PQR. Он является прямоугольным треугольником, значит, применяя основное свойство прямоугольных треугольников, мы можем использовать теорему Пифагора, чтобы найти отрезок QR.

Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы (стороны напротив прямого угла) равен сумме квадратов катетов (остальных двух сторон).

Используем эту формулу:
QR² = PR² + PQ²

Мы знаем, что угол P равен 60 градусов, следовательно, угол Q равен 180 градусов минус 90 градусов минус 60 градусов, то есть 30 градусов.

Теперь найдем значение сторон треугольника PRQ. Застолье, сторона QR будем обозначать за "х".
PR - это гипотенуза треугольника PQR, значит, PQ равно половине PR (так как угол P равен 60 градусов, что делает треугольник равносторонним). Значит, PQ равно PR/2.

Найдем отношение сторон PR и PQ:
PR = PQ * 2

Также, используя угол Q, мы можем записать:
QR = x * cos(30°)

Теперь подставим значения в формулу Пифагора:
(x * cos(30°))² = (PQ * 2)² + PQ²

После подстановки, упрощения и упрощения уравнения мы получаем:
x² * (cos²(30°) - 1) = 4PQ²
x² * (3/4 - 1) = 4PQ²
x² * (-1/4) = 4PQ²
- x²/4 = 4PQ²
-x² = 4 * 4PQ² = 16PQ²

Теперь мы можем найти отрезок PQ. Обозначим его за "y". По теореме Пифагора:
y² = PR² - PQ² = (2y)² - y² = 4y² - y² = 3y²

Отсюда получаем значение PQ:
PQ = √(y²/3) = y/√3

Теперь мы можем подставить значение PQ в уравнение:
-x² = 16PQ²
-x² = 16(y/√3)²
-x² = 16y²/3
-3x² = 16y²

Мы знаем, что PS = 18 см, поэтому PQ + QS = 18 см.
PQ + QR * sin(30°) = 18
PQ + x/2 = 18

Теперь мы можем объединить все уравнения и решить систему уравнений для нахождения x:
-3x² = 16y²
PQ + x/2 = 18

Исходя из системы уравнений, мы можем выразить PQ через y:
PQ = 18 - x/2

Теперь подставим это значение в первое уравнение:
-3x² = 16(y/√3)²
-3x² = 16(y²/3)
-9x² = 16y²
-9x² = 16(18 - x/2)²
-9x² = 16(18 - x/2)(18 - x/2)
-9x² = 16(324 - 18x/2 - 18x/2 + x²/4)
-9x² = 16(324 - 18x + x²/4)

Раскроем скобки и упростим:
-9x² = 16(324 - 36x + x²/4)
-9x² = 5184 - 576x + 4x²
0 = 9x² - 576x + 5184 - 4x²
0 = 5x² - 576x + 5184

Теперь мы имеем квадратное уравнение вида ax² + bx + c = 0. Для решения этого уравнения можно использовать формулу дискриминанта.
Дискриминант D равен b² - 4ac.
Если D > 0, то у уравнения два различных корня.
Если D = 0, то у уравнения один корень.
Если D < 0, то уравнение не имеет корней.

В нашем случае a = 5, b = -576 и c = 5184.
D = (-576)² - 4 * 5 * 5184
D = 331776 - 103680
D = 228096

Так как D > 0, уравнение имеет два различных корня. Для нахождения корней мы можем использовать формулу:
x = (-b ± √D) / (2a)

x₁ = (-(-576) + √228096) / (2 * 5)
x₁ = (576 + 478.56) / 10
x₁ = 1054.56 / 10
x₁ = 105.46

x₂ = (-(-576) - √228096) / (2 * 5)
x₂ = (576 - 478.56) / 10
x₂ = 97.44 / 10
x₂ = 9.744

Таким образом, отрезок QR имеет два значения: 105.46 см и 9.744 см.