В прямоугольном треугольнике один из катетов больше другого в 7 раз. Гипотенуза равна корню 200. Найдите площадь этого треугольника

14

Объяснение:

Обозначим один из катетов треугольника буквой х, второй катет в 7 раз больше, поэтому будет 7х. Гипотенуза равна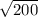

Согласно теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы, т.е. х² +(7х)²=(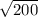)². Решаем данное уравнение:

х² + 49х²=200

50х²=200

х²=4

х=2

Т.е. один катет = 2, второй в 7 раз больше, т.е. 14

Площадь прямоугольного треугольника равна половине произведения катетов, т.е. (2*14)/2=14