В прямоугольном треугольнике катет и гипотенуза равны соответственно 4 см и 6 см.
Найдите синус большего угла острого угла треугольника.
А) Б) В) Г)
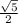
Другие вопросы по теме Геометрия
Популярные вопросы
- От какого слова образовано слово: справлялась ?...
2 - We have some plane we walk our dog 1) are going to 2) going to 3) are...
3 - Найди площадь прямоугольника прямоугольник: длина 2 см., ширина знаю...
2 - Предводителю персов были присущи такие черты характера как...
1 - Разбрать предложения: мал зонтик, да дорог. в чужой монастырь со своим...
3 - Письменное сообщение на тему : о денежной единице любой страны. по окружающему...
1 - Напишите, , заключение реферата на тему ,, правовое государство...
2 - Что бы ты сделал чтобы улучшить работу сердца, можно не научно так чтобы...
1 - Пояснить правописание слова оголённую...
2 - Запишитекст определи границы предложений. вставь пропущенные буквы используя...
3
Г
Объяснение:
Находим второй катет треугольника: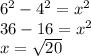
Катет, равный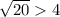 . Также в треугольнике против бОльшей стороны лежит бОльший угол. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе, поэтому
. Также в треугольнике против бОльшей стороны лежит бОльший угол. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе, поэтому 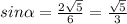 .
.