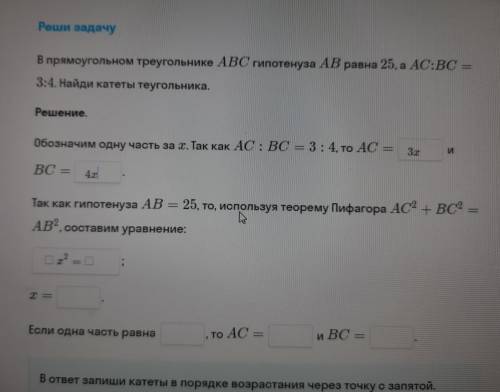
В прямоугольном треугольнике АВС гипотенуза АВ равна 25,а AC:BC= 3:4. Найди катеты теугольника. за решение. Надо расставить цифры по клеточкам это обязательно.

Для решения данной задачи, нам понадобится использовать теорему Пифагора и соотношение между катетами прямоугольного треугольника.

1) Согласно теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. В данной задаче мы знаем, что гипотенуза AB равна 25. Обозначим катеты треугольника через x и y. Тогда можем записать:
x^2 + y^2 = 25^2

2) Зная, что AC:BC = 3:4, можем обозначить AC через 3k, а BC через 4k, где k - некоторая константа. Тогда можем записать:
AC = 3k
BC = 4k

3) Так как треугольник прямоугольный, то можно воспользоваться соотношением между катетами прямоугольного треугольника. Согласно этому соотношению, произведение катетов равно произведению сегментов гипотенузы. То есть:
x*y = AC*BC

Теперь, у нас есть система уравнений на x и y:
x^2 + y^2 = 25^2
x*y = 3k*4k

Давайте пошагово решим эту систему уравнений:

1) Запишем второе уравнение в виде x = (3k*4k)/y
2) Подставим это выражение в первое уравнение:
(3k*4k)/y^2 + y^2 = 625

3) Умножим обе части уравнения на y^2:
12k^2 + y^4 = 625y^2

4) Перенесем все слагаемые в одну часть уравнения:
y^4 - 625y^2 + 12k^2 = 0

5) Это уравнение является квадратным относительно y^2. Решим его с использованием дискриминанта:
D = 625^2 - 4*12k^2

6) Подставим D в формулу дискриминанта и найдем значение y^2:
y^2 = (-625 + √D)/2 или y^2 = (-625 - √D)/2

7) Теперь найдем x, подставив найденное значение y^2 во второе уравнение:
x = (3k*4k)/y

Таким образом, мы получили два возможных значения для катетов прямоугольного треугольника. При подстановке числовых значений для k в эти выражения, мы получим конкретные значения для катетов.