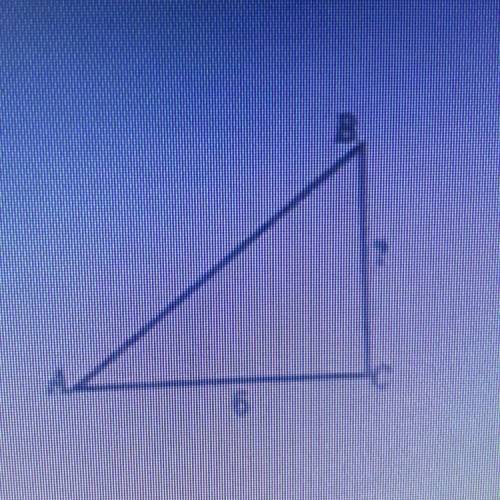
В прямоугольном треугольнике абс ctg A=3/2 , ac=6 , найдите bc
Другие вопросы по теме Геометрия
Популярные вопросы
- Какое число надо прибавить к числу 69,16,71,48 чтобы в сумме получилось...
3 - Для обозначения десятков древние римляне использовали такие цифры x...
1 - Дайте характеристику лития, хлора, фтора, азота по пунктам( ниже) 1....
3 - Вкакую из четырёх сфер общества входят: забота о престарелых,голосование...
3 - 1)обведи синим цветом отрезок ок ,д линна которого равна сумме длин...
3 - План,,слово о полку игореве 9 класс....
3 - Согласие, обида, ссора, улыбка, крик, уважение, злость, терпение, понимание,...
1 - Кто такие землевладельцы? что такое майордом? кто такой феодал? кто...
2 - Обозначить орфограмму в слове ручьи...
3 - Как связана температура тела со скоростью движения его молекул? привидите...
3
1) Тангенс угла A: tg A = противоположный катет / прилежащий катет
2) Котангенс угла A: ctg A = прилежащий катет / противоположный катет
3) Применим основное соотношение ctg A = 1 / tg A
В данном случае, задано, что ctg A = 3/2. Значит, мы можем воспользоваться формулой коэффициента.
4) Так как ctg A = 3/2, то мы можем записать 1/tg A = 3/2. Значит, tg A = 2/3.
Далее, нам дано, что ac = 6 и мы должны найти bc. Здесь нам может быть полезным теорема Пифагора.
5) Запишем теорему Пифагора для треугольника abc: ac² = ab² + bc²
Мы можем заменить ac на 6, так как это значение задано.
6) 6² = ab² + bc²
36 = ab² + bc²
Теперь нам нужно найти ab.
7) Запишем соотношение между tg A и ab: tg A = противоположный катет / прилежащий катет
tg A = ab / bc
Зная, что tg A = 2/3, мы можем записать:
8) 2/3 = ab / bc
Далее, мы можем решить это уравнение относительно ab, используя полученное значение ab и подставляя его в наше уравнение из шага 6.
9) Решим уравнение:
2/3 = ab / bc
Умножим обе части уравнения на bc:
2/3 * bc = ab
Теперь, мы можем подставить это значение ab в наше уравнение из шага 6:
36 = (2/3 * bc)² + bc²
Далее, мы можем упростить это уравнение и решить его.
36 = 4/9 * bc² + bc²
Приведем подобные слагаемые:
36 = (4/9 + 1) * bc²
Упростим выражение в скобках:
36 = (13/9) * bc²
Умножим обе части уравнения на 9/13:
(36 * 9/13) = bc²
Вычислим:
36 * 9 / 13 = 324 / 13 = 24.923
Теперь, найдем квадратный корень от обеих частей уравнения:
√(324 / 13) = √24.923
bc = 4.99
Таким образом, bc ≈ 4.99.