.В прямаугольной трапеции ABCD с оснаванием AD и прямым углом A известно,что AB=8и угол D=30°Найдите длину вектора C
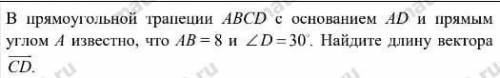
Другие вопросы по теме Геометрия
Популярные вопросы
- Перевод текста и вставте то что нужно в точках there isn t a table...
1 - Постройте сложноподчиненное предложение, подобрав к каждому главному...
1 - Почему финикию называют «геркулесовы столбы»...
2 - Сделать звуко-буквенный разбор труд, дров, прут...
2 - 13 м в квадрате 2 см в квадрате сколько в...
3 - Вычислить нормальность раствора, на титрование 10 мл которого израсходовано...
1 - Вкоробке 100 жетонов,отличающихся лишь цветом: 20 красных,20 жёлтых,20...
2 - Мудрая черепаха предлагает для тренировки памяти и внимания пронумеруй...
1 - Какие из уравнений имеют два корня? а) x2=4 (x-2)(x+2)=0 (x-2)2=0...
2 - Сравнить сказки! спящая царевна, спящая красавица, сказка о мертвой...
3
Поскольку у нас прямоугольная трапеция, будем использовать свойство такой фигуры: диагонали трапеции равны по длине.
По условию задачи, известно, что AB=8. Мы знаем также, что угол D равен 30°.
Рассмотрим треугольник ABD. Так как мы имеем прямую трапецию, то в этом треугольнике у нас есть прямой угол (угол D), и у нас есть одно из оснований трапеции (AB).
Мы можем воспользоваться тригонометрической функцией синус для нахождения длины диагонали BD. Округлим ответ до второго знака после запятой.
sin(D) = противолежащий катет / гипотенуза
sin(30°) = BD / AB
Тогда BD = AB * sin(30°)
BD = 8 * sin(30°)
Для решения этой задачи, нам понадобится значение синуса 30°. Мы можем использовать таблицу значений тригонометрических функций или калькулятор.
sin(30°) = 0.5
Теперь мы можем подставить это значение в формулу:
BD = 8 * 0.5
BD = 4
Таким образом, длина диагонали BD равна 4.
Теперь рассмотрим треугольник BCD. У нас уже есть диагональ BD, которая равна 4, и угол D, который равен 30°. Мы можем снова воспользоваться тригонометрической функцией синус для нахождения длины диагонали BC. Округлим ответ до второго знака после запятой.
sin(D) = противолежащий катет / гипотенуза
sin(30°) = BC / BD
Тогда BC = BD * sin(30°)
BC = 4 * sin(30°)
sin(30°) = 0.5
BC = 4 * 0.5
BC = 2
Таким образом, длина диагонали BC равна 2.
В итоге, длина вектора C (диагональ AC) равна сумме длин оснований AD и BC:
AC = AD + BC
AC = 8 + 2
AC = 10
Итак, длина вектора C равна 10.