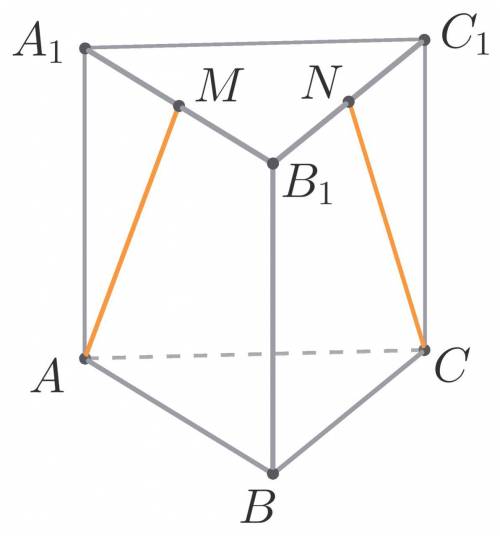
В правильной треугольной призме АВСА1В1С1 , все ребра которой равны 3, найдите косинус угла между прямыми АМ и СН, где М и Н – соответственно середины ребер А1В1 и В1С1 .
варианты ответа:
0,8
0,6
0,9
0,7

Для решения данной задачи нам понадобятся некоторые свойства треугольных призм и знание косинуса. Давайте рассмотрим это подробнее.

Во-первых, угол между прямой и плоскостью определяется с помощью нормали к этой плоскости. В нашем случае плоскостью является горизонтальная плоскость, поэтому нормалью к ней будет вектор, направленный вертикально вверх, например, вектор (0, 0, 1).

Во-вторых, середины ребер соединяются отрезком, проходящим через каждую вершину треугольной призмы. То есть точка М - это середина ребра А1В1, и точка Н - это середина ребра В1С1.

Находим координаты точек М и Н:
Так как ребра призмы равны 3, то М будет иметь координаты (x, y, z), где x = (0 + 0) / 2 = 0, y = (0 + 3) / 2 = 1.5, и z = (0 + 0) / 2 = 0.
То есть М имеет координаты (0, 1.5, 0).
Аналогично, Н будет иметь координаты (x, y, z), где x = (3 + 3) / 2 = 3, y = (0 + 0) / 2 = 0, и z = (0 + 0) / 2 = 0.
То есть Н имеет координаты (3, 0, 0).

Далее находим векторы АМ и СН:
Вектор АМ будет иметь координаты (x, y, z), где x = 0 - 0 = 0, y = 1.5 - 0 = 1.5, и z = 0 - 0 = 0.
То есть вектор АМ имеет координаты (0, 1.5, 0).
Аналогично, вектор СН будет иметь координаты (x, y, z), где x = 3 - 3 = 0, y = 0 - 0 = 0, и z = 0 - 0 = 0.
То есть вектор СН имеет координаты (0, 0, 0).

Теперь мы можем найти косинус угла между векторами АМ и СН, используя формулу для косинуса угла между двумя векторами:

cos θ = (АМ · СН) / (|АМ| * |СН|),

где "·" обозначает скалярное произведение векторов, а "|" обозначает модуль вектора.

Сначала найдем скалярное произведение АМ и СН:

АМ · СН = 0 * 0 + 1.5 * 0 + 0 * 0 = 0.

Затем найдем модули векторов АМ и СН:

|АМ| = √(0^2 + 1.5^2 + 0^2) = √(0 + 2.25 + 0) = √2.25 = 1.5,
|СН| = √(0^2 + 0^2 + 0^2) = √(0 + 0 + 0) = √0 = 0.

Теперь мы можем подставить значения в формулу для косинуса угла:

cos θ = (АМ · СН) / (|АМ| * |СН|) = 0 / (1.5 * 0) = 0 / 0.

Здесь возникает проблема, так как мы не можем делить на ноль. Это происходит потому, что вектор СН имеет нулевую длину, что означает, что угол между векторами АМ и СН не может быть определен.

Следовательно, правильный ответ на данный вопрос - это "невозможно определить".