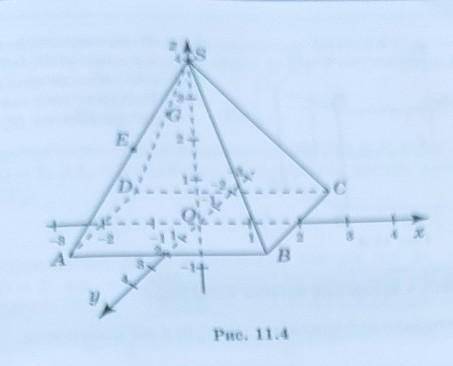
В правильной четырехугольной пирамиде CABCD стороны основания и высота равны 4 см. Точка Е - середина ребра СА ( рис. 11.4 ) . Найдите расстояние от точки Е до плоскости SBC . РЕШИТЕ С ОБЪЯСНЕНИЕМ, очень нужно до ЗАВТРА

Условие конечно неверно записано, но благо из рисунка все понятно ))

Оси на нем обозначены.

Координаты точек

Е (-1;1;2)

S(0;0;4)

B(2;2;0)

C(2;-2;0)

Уравнение плоскости SBC

ax+by+cz+d=0

Подставляем координаты точек S B C

4c+d=0

2a+2b+d=0

2a-2b+d=0

Откуда b =0

Пусть d = -4 , тогда с=1, а =2

Искомое уравнение

2х+z-4 =0

k = √(2^2+1^2)=√5

Нормальное уравнение плоскости

2x/√5+z/√5-4/√5 =0

Для нахождения искомого расстояния подставляем координаты точки Е в нормальное уравнение плоскости

| Е; SBC | = | -2/√5+2/√5-4/√5 | = 4/√5

4 / √5  ...........

Объяснение: