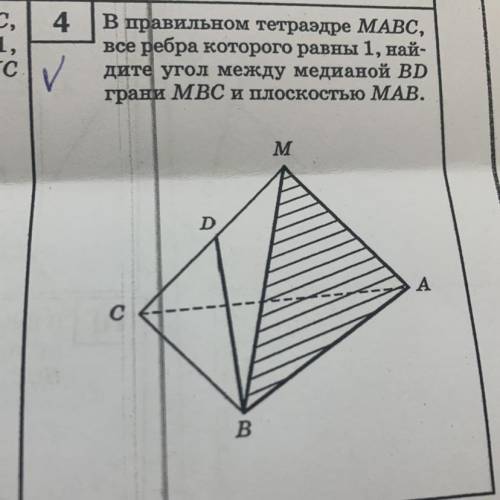
В правильном тетраэдре MABC, все рёбра которого равны 1, найдите угол между медианой BD грани MBC и плоскостью MAB

Добрый день! Представим, что мы учимся геометрии и решаем задачу на построение угла между медианой и плоскостью в правильном тетраэдре. Давайте разберемся, как найти этот угол.

Сначала, чтобы понять, что такое медиана и плоскость в данной задаче, вспомним некоторые определения. Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В нашем случае, медиана BD грани MBC - это отрезок, соединяющий вершину D с серединой отрезка BC (обозначим эту середину точкой E).

Чтобы найти угол между медианой BD и плоскостью MAB, мы можем воспользоваться свойством скалярного произведения векторов. Скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними. Если мы найдем скалярное произведение медианы BD и нормали к плоскости MAB, то сможем найти искомый угол.

Давайте найдем векторы BD и нормаль к плоскости MAB.

Вектор BD - это вектор, направленный от точки B к точке D. В нашем случае, все рёбра тетраэдра равны 1, поэтому длина вектора BD также равна 1. Ориентированный вектор BD может быть найден как разность координат точек D и B, то есть:
BD = (xD - xB, yD - yB, zD - zB).

Изображение тетраэдра не дано, поэтому необходимо привести примерное решение задачи. Предположим, что вершина M находится в начале координат (0,0,0), вершина A имеет координаты (1,0,0), вершина B - (0,1,0), а вершина C - (0,0,1).

Теперь найдем нормаль к плоскости MAB. Нормаль к плоскости - это вектор, перпендикулярный плоскости. Для ее нахождения можно воспользоваться произведением векторов. Для этого найдем векторное произведение двух векторов: AB и AM.

Вектор AB - это вектор, направленный от точки A к точке B. В нашем случае, длина вектора AB также равна 1. Ориентированный вектор AB может быть найден как разность координат точек B и A, то есть:
AB = (xB - xA, yB - yA, zB - zA).

Вектор AM - это вектор, направленный от точки A к точке M (начало координат). В нашем случае, координаты точки M равны (0,0,0). Ориентированный вектор AM может быть найден как разность координат точек M и A, то есть:
AM = (xM - xA, yM - yA, zM - zA).

Теперь найдем искомый угол. Для этого рассчитаем скалярное произведение вектора BD и нормали к плоскости MAB:
BD * normal(MAB) = |BD| * |normal(MAB)| * cos(угла между BD и normal(MAB)).

|BD| = 1 (так как длина отрезка BD равна 1), тогда скалярное произведение будет равно:
BD * normal(MAB) = |normal(MAB)| * cos(угла между BD и normal(MAB)).

Таким образом, чтобы найти искомый угол, нужно найти значение скалярного произведения BD и normal(MAB), а затем вычислить арккосинус от этого значения.

К сожалению, в задаче не даны координаты точек D и E, поэтому невозможно точно рассчитать нормаль к плоскости MAB и найти искомый угол. Для получения точного численного значения угла необходимо знать координаты всех вершин тетраэдра и точки D. Однако, вы можете предположить некоторые координаты этих точек и рассчитать угол с помощью операций, которые мы только что обсудили.

Если у вас есть какие-либо предположения о координатах вершин тетраэдра и точки D, я могу помочь вам рассчитать искомый угол.