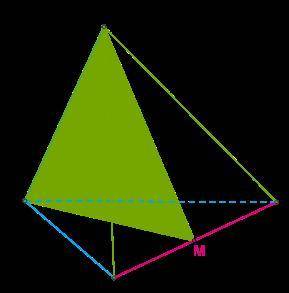
В пирамиде DABC точка M - середина ребра CB. Известно, что AC=AB; DC=DB. Найдите угол между прямой CB и плоскостью AMD. ответ запишите в градусах.

Добрый день! Давайте решим эту задачу пошагово.

Из условия задачи известно, что точка М является серединой ребра CB в пирамиде DABC. Также сказано, что AC равна AB, а DC равна DB.

Чтобы найти угол между прямой CB и плоскостью AMD, нам нужно знать уравнение этой плоскости. Построим его.

Для начала построим прямую, заданную точкой М и направляющим вектором CB. Прямая будет иметь вид:

r = М + t(CB),

где r - радиус-вектор любой точки на прямой, М - радиус-вектор точки М, а t - параметр, меняющийся от 0 до 1.

Теперь найдем уравнение плоскости AMD. Для этого нам понадобится векторное произведение:

n = AM x MD,

где n - нормальный вектор плоскости AMD, AM - вектор, соединяющий точки A и M, MD - вектор, соединяющий точки M и D.

Теперь найдем угол между вектором CB и нормальным вектором плоскости. Для этого воспользуемся формулой:

cos(θ) = (CB * n) / (|CB| * |n|),

где θ - угол между вектором CB и нормальным вектором плоскости AMD, CB * n - скалярное произведение векторов CB и n, |CB| и |n| - длины векторов CB и n.

Таким образом, мы найдем косинус угла θ. Чтобы получить значение угла θ, возьмем обратный косинус найденного значения косинуса: θ = acos(cos(θ)).

Теперь приступим к вычислениям.

Найдем радиус-вектор точки М. Мы знаем, что М - середина ребра CB, поэтому можно записать:

М = (C + B) / 2.

Дальше найдем радиус-вектор точки AM:

AM = A - М.

Также найдем радиус-вектор точки MD:

MD = D - М.

Теперь найдем нормальный вектор плоскости AMD, используя векторное произведение:

n = AM x MD,

где AM = (AMx, AMy, AMz) и MD = (MDx, MDy, MDz).

Вычислим определитель следующей матрицы:

| i j k |
| AMx AMy AMz |
| MDx MDy MDz |,

где i, j, k - единичные векторы, AMx, AMy, AMz - компоненты вектора AM, а MDx, MDy, MDz - компоненты вектора MD.

Раскроем определитель по первому столбцу:

n = (AMy * MDz - AMz * MDy) * i - (AMx * MDz - AMz * MDx) * j + (AMx * MDy - AMy * MDx) * k,

где i, j, k - начальные компоненты вектора n.

Теперь найдем скалярное произведение векторов CB и n:

CB * n = (CBx * (AMy * MDz - AMz * MDy) - CBy * (AMx * MDz - AMz * MDx) + CBz * (AMx * MDy - AMy * MDx)).

Теперь вычислим значения длин векторов CB и n:

|CB| = √(CBx² + CBy² + CBz²),

|n| = √((AMy * MDz - AMz * MDy)² + (AMx * MDz - AMz * MDx)² + (AMx * MDy - AMy * MDx)²).

Наконец, найдем косинус угла θ:

cos(θ) = (CB * n) / (|CB| * |n|).

Теперь возьмем обратный косинус найденного значения косинуса, чтобы найти угол θ:

θ = acos(cos(θ)).

Таким образом, мы найдем значение угла между прямой CB и плоскостью AMD в градусах.

Пожалуйста, используйте эти формулы для решения задачи. Если у вас возникнут трудности с вычислениями или пониманием решения, я всегда готов помочь.