В пирамиде ABCS ребро AS перпендикулярно основанию ABС и равно 4. Треугольник ABC равносторонний со стороной 2. Найдите высоту AH, проведенную к грани SBC. В ответе укажите значение 19·A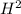

Другие вопросы по теме Геометрия
Популярные вопросы
- Составить программу на паскале, которая в двумерном массиве определяет...
1 - Решить примеры шестого класса номер 529 вычисление 1 класс по действиям...
3 - 1. в столовую 32 коробки фруктов. в 14 коробках были апельсины...
3 - Спільне в відмінне між байкою та притчею (бажано, у вигляді таблиці,...
1 - Ть скласти 2 реченя з часткою es і 2без частки es...
2 - Как ты понимаешь смысл выражений муки совести , угрызения совести...
1 - Асоціативний кущ дл романтизму...
2 - Сколько лет комендант и комендантша живут в крепости? сколько у...
3 - Прощальный блеск зари на небе догорал(синтаксический разбор)...
3 - Жауынгер сақтар жайлытарихшылар не айтады? i. парсы : «құдіретті...
3
Пусть B - начало координат
Ось X - BC
Ось Y - перпендикулярно X в направлении A
Ось Z - перпендикулярно ABC в направлении S
Координаты точек
С ( 2;0;0)
S ( 1; √3;4)
A ( 1; √3;0)
Уравнение плоскости SBC ( проходит через начало координат )
ax + by + cz = 0
Подставляем координаты точек S C
2a=0
a+√3b + 4c =0
Откуда a=0
Пусть b = 4/(√3) тогда с = -1
Уравнение плоскости SBC
4y/√3 - z = 0
Нормальное уравнение плоскости
k= √(16/3+1) = √(19/3)
4y/√19 - √3z/√19 =0
Подставляем координаты точки A в нормальное уравнение для нахождения расстояния от точки А до плоскости SBC ( оно же длина высоты AH )
4 * √3 / √19
По условию просят 19 * (4√3/√19 ) ^2 = 48