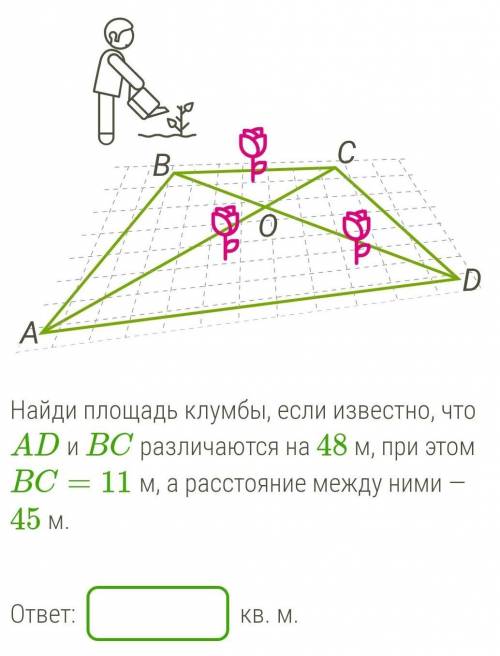
В парке при музее решили разбить клумбу в форме четырёхугольника. Две стороны этой клумбы (AD и BC), если бы можно было продлить их на бесконечную длину, никогда б не пересеклись. Другие две (AB и CD), если бы можно было продлить их на бесконечную длину, сошлись бы когда-нибудь одной точке. Когда попарно соединяли несмежные вершины этой клумбы дорожками из ракушек, то выяснилось, что длина этих дорожек вышла абсолютно одинаковой. ​

анастатья    2   14.03.2021 22:06    57