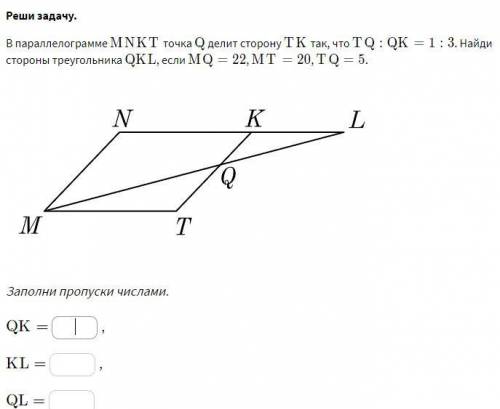
В параллелограмме MNKT MNKT точка QQ делит сторону TKTK так, что TQ:QK = 1:3TQ:QK=1:3 . Найди стороны треугольника QKLQKL , если MQ = 22MQ=22 , MT = 20MT=20 , TQ = 5TQ=5 .
Другие вопросы по теме Геометрия
Популярные вопросы
- Составте которую можно решить уравнение в 5 классе...
1 - Жили дед и баба была у них курочка ряба курочка несет каждое второе яичко...
1 - Яке це речення просте чи складне? чоловіки й жінки (особливо на буковині,...
1 - Выражения 25a•4b и найти его значение, если a=74,b=3...
1 - Кончилась теплая летняя ночь. кончилась теплая летняя ночь. занимается над...
2 - Как пишутся слова: (девицы)красавиц.. ( (кресло)качалка ( (далеко)далеко...
3 - Как условными знаками обозначается северное сияние. 4 класс. . заранее...
2 - Не большой рассказ на тему представьте что вы вместе с друзьями и вы ученые...
1 - Морфологический разбор слова звуков...
3 - Решите уравнения: 1)6х+5х-16=28 2)8y-y+12=40 3)528: p-24=64...
1
Заметим, что отношение TQ:QK = 1:3 говорит нам, что TQ составляет 1/4 от всей стороны TK (поскольку QK составляет 3/4 от TK).
Первым шагом рассмотрим сторону KM. Согласно свойству параллелограмма, KM равно стороне NT. Из условия задачи, известно, что NT = 22, значит KM тоже равно 22.
Теперь, чтобы найти сторону KL, мы можем использовать теорему Пифагора в треугольнике MQK.
Зная стороны MQ и MK, мы можем найти сторону QK с помощью теоремы Пифагора:
MK^2 = MQ^2 + QK^2
22^2 = 20^2 + QK^2
484 = 400 + QK^2
QK^2 = 84
QK = √84
QK = 2√21
Теперь, мы знаем, что QK = 2√21. Согласно условию задачи, TQ составляет 1/4 от TK, а значит TQ = TK/4. Подставляя известные значения в уравнение:
TQ = 5 = TK/4
TK = 20
Теперь, мы можем найти KL, используя уравнение: KL = TK - QK
KL = 20 - 2√21
Таким образом, стороны треугольника QKL равны:
QK = 2√21
KL = 20 - 2√21