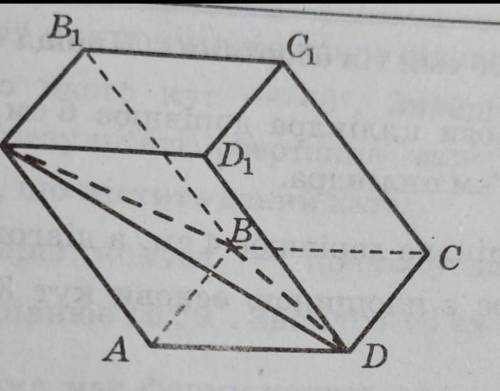
В параллелепипеде ABCDA1B1C1D1 проведено сечение через прямую BD и точку A1 (рис.17). Найдите объем параллелепипеда, если объем пирамиды A1ABD равен V. С ОБЪЯСНЕНИЕМ !
Другие вопросы по теме Геометрия
Популярные вопросы
- Как называется сбор в пользу государства части урожая и приплода скота?...
1 - Возможно ли существование современной биосфер без грибов и растений...
3 - Вставить артикли там, где это необходимо don t don t coffee i ve you can...
1 - Какой глагол изменяется по числам и ? накопим горит дремала журчали. какой...
2 - Прочтите отрывок из письма.в каком году это письмо появилось? наконец прогнали...
3 - Какое количество вещества соответствует 80г оксида магния mgo? ? ответ :...
1 - Заменил слово щедро(из 4-го предложения)близким по значению словом, записи...
3 - Отзыв экзюпери маленький принц ! (именно отзыв а не краткий пересказ)...
1 - Какой будет ответ укажи падежи имен существительных пьесу о друге в берег...
1 - Період коливань маятника дорівнює 10 с. визначте частоту його коливань...
1
Параллелепипед ABCDA1B1C1D1 и пирамида ABDA1 имеют общую высоту - это перпендикуляр H, опущенный из общей вершины A1 на плоскость ABC.
Из формулы объёма пирамиды V = (1/3)SoH выразим Н.
H = 3V/So. Здесь So – площадь треугольника АВD.
У параллелепипеда площадь S основания в 2 раза больше.
То есть: S = S(ABCD) = 2So.
Объём параллелепипеда Vп = SH = 2So*(3V/So) = 6V.
ответ: объём параллелепипеда Vп = 6V.