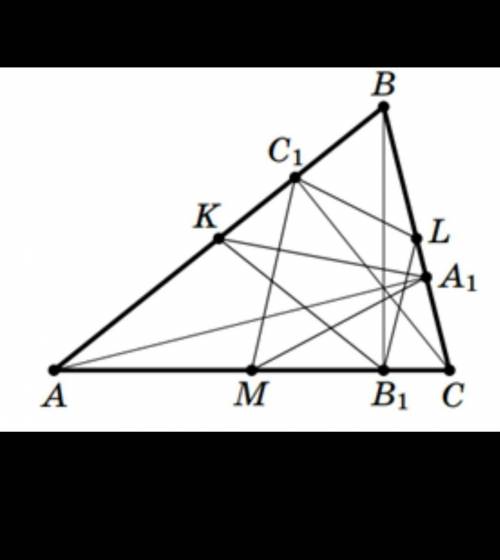
В остроугольном треугольнике ABC проведены высоты AA1, BB1 и CC1. Точки K, L и M — середины сторон AB, BC и CA соответственно. Докажите, что длина замкнутой ломаной KB1LC1MA1K равна периметру треугольника ABC.

Для начала, давайте вспомним некоторые известные свойства остроугольных треугольников и высотах.

Свойство 1: В остроугольном треугольнике каждая высота перпендикулярна соответствующей стороне.
Свойство 2: В остроугольном треугольнике точка пересечения высот делит их на две части, причем каждая часть равна сумме других двух.

Теперь перейдем к решению.

Предположим, что длина стороны AB равна a, стороны BC равна b, а стороны CA равна c.

1. Докажем, что треугольники KB1L и MC1K равны по площади.
- Заметим, что LM = (1/2)*c и KL = (1/2)*a. Используя свойство 2 остроугольных треугольников, мы можем сказать, что BL = (1/2)*b и BM = (1/2)*b.
- Из свойства 1 следует, что площадь треугольника KB1L равна (1/2)*KB1*BL, а площадь треугольника MC1K равна (1/2)*MC1*KC1.
- Подставим известные значения и получим, что площади равны (1/2)*((1/2)*c)*((1/2)*b) = (1/8)*bc.
- Таким же образом, можно доказать, что площади треугольников LB1C и AK1M тоже равны (1/8)*bc.

2. Докажем, что треугольники KB1L и LB1C равны по площади.
- Заметим, что KA = (1/2)*c и KC = (1/2)*a. Используя свойство 2 остроугольных треугольников, мы можем сказать, что AL = (1/2)*b и LC = (1/2)*b.
- Из свойства 1 следует, что площадь треугольника KB1L равна (1/2)*KB1*BL, а площадь треугольника LB1C равна (1/2)*LB1*BC1.
- Подставим известные значения и получим, что площади равны (1/2)*((1/2)*c)*((1/2)*b) = (1/8)*bc.
- Таким же образом, можно доказать, что площади треугольников LB1C и AK1M тоже равны (1/8)*bc.

3. Теперь сложим площади треугольников KB1L, MC1K, LB1C и AK1M:
- (1/8)*bc + (1/8)*bc + (1/8)*bc + (1/8)*bc = (1/2)*bc + (1/2)*bc = bc
- Таким образом, сумма площадей треугольников равна bc.

4. Сумма площадей треугольников KB1L, MC1K, LB1C и AK1M равна периметру треугольника ABC.
- Периметр треугольника ABC равен a + b + c, а площади треугольников KB1L, MC1K, LB1C и AK1M равны bc.
- Таким образом, сумма площадей равна периметру треугольника ABC.

Таким образом, длина замкнутой ломаной KB1LC1MA1K равна периметру треугольника ABC.