В остроугольном треугольнике ABC проведена высота BH. Из точки H на стороны AB и BC опустили перпендикуляры HL и HK соответственно. BH=a, 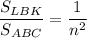 . 1. Доказать, что треугольники LBK и ABCподобны.
. 1. Доказать, что треугольники LBK и ABCподобны.
2. Найти радиус окружности, описанной около треугольника ABC.
Другие вопросы по теме Геометрия
Популярные вопросы
- Не понимаю , завтра уже проверят...
2 - Какова формулировка и запись закона электромагнитной индукции...
3 - Доклад по теме: борьба с эпифитотией . 7 класс. 21 ....
1 - Кімдер алғаны туралы семантикалық картаны толтыр. түсіндіріп айт....
1 - Твір на тему подолати в собі раба за твором в.дрозда білий кінь шептало...
1 - Якими чинниками обумовлена подібність ландшафтів укрфїни і світу...
2 - 1) оценка произведения чистый понедельник критиками. 2) эмоциональное...
1 - Синквейн к слову проишествие...
2 - Дерев яний брусок витісняє собою 0,0005м³. скільки важить брусок?...
3 - Катер отплыл от пристани а и проплыл против течения т часов. собственная...
2
BLHK - вписанный четырехугольник (т.к. противоположные углы прямые)
Прямой угол опирается на диаметр BH, AC - касательная (т.к. AC⊥BH)
LHA =LH/2 (угол между касательной и хордой) =LKH
A =90-LHA =90-LKH =BKL
△ABC~△KBL (по двум углам)
S(ABC)/S(KBL) =k^2 => k=n
R_KBL =BH/2 =a/2
R_ABC/R_KBL =k =n => R_ABC =na/2