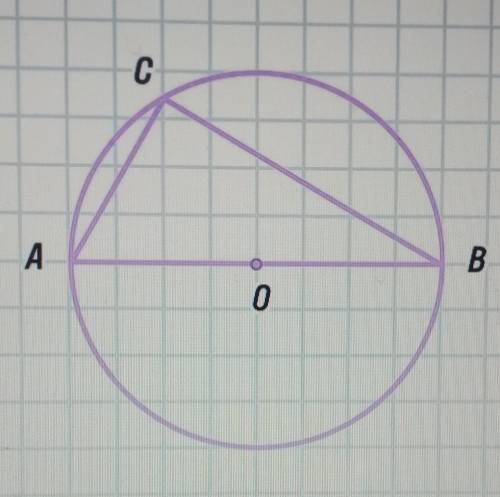
В окружности с центром о вписан треугольник с вершинами A B и c. Точка O лежит на стороне AB. Найди угол ABC если угол бас равен 60 градусов

Добрый день!

Для решения данной задачи, нам необходимо использовать свойства вписанных углов и свойств треугольников.

Итак, пусть угол ABC равен x. Также, из условия задачи, угол BAC равен 60 градусов.

В связи с тем, что треугольник ABC вписан в окружность, угол BAC является половиной центрального угла, соответствующего дуге BC окружности. Значит, центральный угол BOC равен удвоенному углу BAC (т.е. 120 градусов).

Используя свойство центральных углов, получаем, что угол BOC равен половине угла на центральное пересечение, т.е. половине суммы углов вокруг точки O:

BOC/2 = (180 - x) + 120
BOC/2 = 300 - x

Затем, используя свойство угла на окружности, получаем, что угол вписанный в данную дугу BC равен половине центрального угла BOC:

(180 - x)/2 = (300 - x)/2
180 - x = 300 - x
180 = 300

Полученное уравнение 180 = 300 невозможно, так как оно не имеет решений.

Следовательно, отсутствует корректный ответ на данный вопрос.

Надеюсь, это решение и объяснение помогут вам лучше понять задачу. Если у вас есть еще вопросы - не стесняйтесь задавать их!