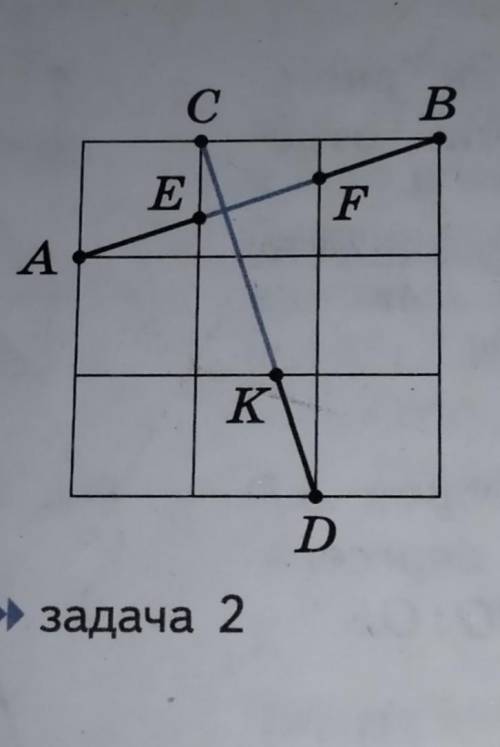
В квадрате 3х3 клетки провели отрезки AB и CD так, как это показано на рисунке. Найдите отношение отрезков EF и CK.

Привет! Я рад выступить в роли твоего школьного учителя и помочь решить эту задачу.

Для начала, давай взглянем на квадрат 3x3 клетки и отрезки AB и CD. На рисунке мы видим, что отрезки AB и CD разбивают квадрат на четыре треугольника.

Теперь давай рассмотрим отрезок EF. Обрати внимание, что EF - это диагональ квадрата. Так как у нас квадрат 3x3, мы можем использовать теорему Пифагора для найти длину диагонали.

Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. В данном случае, гипотенуза - это отрезок EF, а катеты - это отрезки EA и AF.

Теперь вспомним, что все стороны квадрата равны друг другу. Значит, отрезки EA и AF равны. Если мы обозначим длину одного из них как х, то длина EF будет равна 2х (длина диагонали квадрата равна произведению длины стороны на √2).

Давай теперь приступим к расчетам. Пусть длина стороны квадрата будет L. Значит, длина отрезка EA или AF равна L/3. Тогда длина диагонали EF будет равна 2х = 2(L/3) = 2L/3.

Теперь давай рассмотрим отрезок CK. Обрати внимание, что отрезок CK - это диагональ треугольника. Так как у нас треугольник прямоугольный с катетами CK и CK, мы можем снова использовать теорему Пифагора.

Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. В данном случае, гипотенуза - это отрезок CK, а катеты - это отрезки CK и CK.

Теперь обрати внимание, что отрезки CK и CK равны (они являются сторонами квадрата). Пусть длина каждого из них будет равна х. Тогда длина гипотенузы CK будет равна √(х^2 + х^2) = √2х^2 = √2*(х^2) = х*√2.

Теперь давай сравним длины отрезков EF и CK. Мы установили, что длина диагонали EF равна 2L/3, а длина диагонали CK равна х*√2.

Чтобы найти отношение отрезков EF и CK, нам нужно разделить длину отрезка EF на длину отрезка CK:

(2L/3) / (х*√2) = (2/3L) * (№2/х) = (2/3)*(№2/х) * (х/х) = (2*№2*х) / (3*х*√2) = (2*№2) / (3*√2) = (2/3) * (№2/√2) = (2/3) * (№2/№2) = 2/3.

Таким образом, отношение отрезков EF и CK равно 2/3.