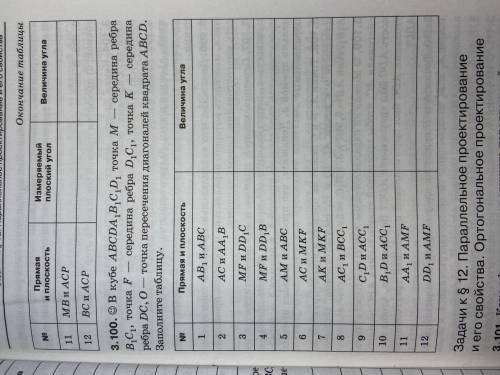
В кубе ABCDA1B1C1D1 точка М - середина ребра B1C1, точка F - середина ребра D1C1, точка К - середина ребра DC. O - точка пересечения диагоналей квадрата ABCD. Заполните таблицу.

Давайте разберемся с этим вопросом по шагам.

1. Для начала нужно определить, какие точки нам даны. В данном случае у нас есть точки М, F, К и O, а также точки A, B, C, D, A1, B1, C1 и D1, которые являются вершинами куба.

2. Теперь давайте поймем, какие сведения известны нам о кубе. Мы знаем, что точка М - середина ребра B1C1. Это означает, что отрезок B1C1 делится пополам точкой М. То есть, если мы соединим точку B1 с точкой C1, то от точки B1 до точки М будет равно от точки М до точки C1, или BM = MC1.

3. В следующий раз, мы знаем, что точка F - середина ребра D1C1. По аналогии с предыдущим шагом, от точки D1 до точки F будет равно от точки F до точки C1, или DF = FC1.

4. Также нам известно, что точка К - середина ребра DC. Это означает, что отрезок DC делится пополам точкой К. То есть, DK = KC.

5. Теперь давайте рассмотрим точку O, которая является точкой пересечения диагоналей квадрата ABCD. Зная, что ABCD - это куб, мы можем сказать, что все его грани являются квадратами. Из свойств квадратов, мы знаем, что диагонали квадрата перпендикулярны и делятся пополам. Таким образом, точка O будет серединой отрезка AC (так как AC - это диагональ квадрата ABCD). Итак, AO = OC.

Теперь давайте заполним таблицу с полученными данными:

| Название точки | Длина отрезка |
|--------------|--------------|
| М | BM = MC1 |
| F | DF = FC1 |
| К | DK = KC |
| O | AO = OC |

Таким образом, мы заполнили таблицу с длинами отрезков в кубе ABCDA1B1C1D1.