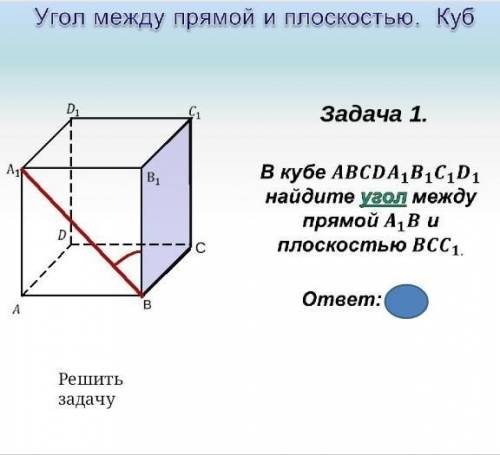
В кубе A, B, C, D, A1, B1, C1, D1 найдите угол между прямой A1B и плоскостью BCC1​

Для решения данной задачи, нужно разобраться в том, как найти угол между прямой и плоскостью.

Во-первых, мы знаем, что плоскость задается уравнением. В данном случае плоскость BCC1 задается точками B, C и C1.

Уравнение плоскости можно найти используя точку B и два вектора, лежащих в плоскости. Возьмем, например, вектор BC и вектор BC1.

Вектор BC можно найти как разность координат точек B и C:
BC = C - B = (0, 0, 1) - (1, 0, 1) = (-1, 0, 0).

Аналогично, вектор BC1 можно найти как разность координат точек BC и C1:
BC1 = C1 - B = (0, 1, 1) - (1, 0, 1) = (-1, 1, 0).

Теперь, у нас есть точка прямой A1B - точка A1 (1, 1, 0) и вектор направления этой прямой, который можно найти как разность координат точек A1 и B:
A1B = B - A1 = (1, 0, 1) - (1, 1, 0) = (0, -1, 1).

Затем, чтобы найти угол между прямой A1B и плоскостью BCC1, нужно найти угол между вектором направления прямой A1B и нормалью плоскости BCC1.

Нормаль плоскости, в данном случае, может быть найдена как векторное произведение векторов BC и BC1:
n = BC * BC1 = (-1, 0, 0) * (-1, 1, 0) = (0, 0, -1).

Теперь, чтобы найти угол между вектором A1B и нормалью плоскости, мы можем использовать следующую формулу:
cos(theta) = (A1B * n) / (||A1B|| * ||n||),

где A1B - вектор направления прямой A1B, n - нормаль плоскости, и || || обозначает длину вектора.

Теперь, подставим все значения и рассчитаем угол:
cos(theta) = ((0, -1, 1) * (0, 0, -1)) / (sqrt(0^2 + (-1)^2 + 1^2) * sqrt(0^2 + 0^2 + (-1)^2)).
cos(theta) = (0 + 0 + 1) / (sqrt(2) * sqrt(1)) = 1 / sqrt(2).

Извлекая корень из 2, получаем:
theta = arccos(1 / sqrt(2)) = arccos(sqrt(2) / 2) = π/4.

Таким образом, угол между прямой A1B и плоскостью BCC1 равен π/4 или 45 градусов.