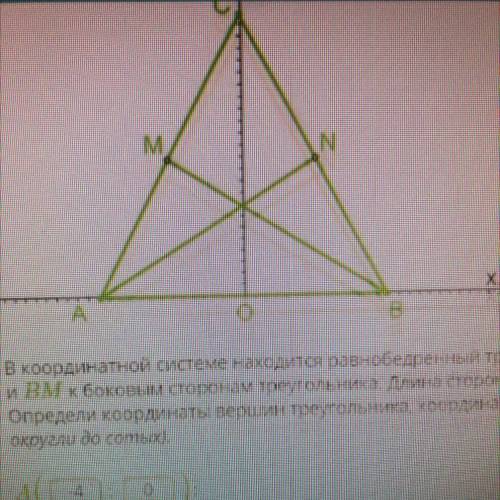
В координатной системе находится равнобедренный треугольник ABC (AC=BC). Проведены медианы AN и BM к боковым сторонам треугольника. Длина стороны AB = 8, а высоты CO = 6. Определи координаты вершин треугольника, координаты точек M и N и длину медиан AN и BM (oтвет округли до сотых)
Найти N, M, AN,BM

Чтобы решить эту задачу, мы можем использовать свойства равнобедренного треугольника и медиан.

Для начала, давайте определим координаты вершин треугольника A, B и C.
Так как сторона AB имеет длину 8, это означает, что расстояние между точками A и B на координатной оси x равно 8.
Предположим, точка A имеет координаты (x₁, y₁) и точка B имеет координаты (x₂, y₂).

Длина стороны AB может быть найдена по формуле расстояния между двумя точками:
AB = √((x₂ - x₁)² + (y₂ - y₁)²)

Мы также знаем, что сторона AC равна стороне BC (равнобедренный треугольник).
Таким образом, точки A и B имеют одинаковые координаты для y: y₁ = y₂.

У нас также есть информация, что длина высоты CO равна 6.
Так как высота проведена к стороне AB, точка C должна лежать на вертикальной прямой, проходящей через середину стороны AB.
Середина стороны AB является точкой с координатами ((x₁ + x₂)/2, (y₁ + y₂)/2).

Теперь давайте найдем координаты вершины C.
Если мы знаем, что точка C лежит на прямой с координатами ((x₁ + x₂)/2, (y₁ + y₂)/2) и имеет длину высоты 6, мы можем найти координаты точки C.

Также давайте обозначим координаты точек N и M как (x₃, y₃) и (x₄, y₄) соответственно.

Теперь, чтобы найти координаты вершины треугольника C, мы можем использовать теорему Пифагора.
Так как мы знаем длину стороны AB (8) и длину стороны CO (6), мы можем найти длину стороны AO (и BO), используя теорему Пифагора.
Так как треугольник ABC равнобедренный, медианы AN и BM являются высотами данного треугольника, поэтому медианы перпендикулярны сторонам и проходят через точку пересечения.

Аналогично, длина медиан AN равна длине высоты CO, то есть 6.

Поэтому координаты точек N и M могут быть найдены, используя середины соответствующих сторон треугольника ABC.

Итак, чтобы решить эту задачу, нам нужно найти:
- Координаты вершин треугольника A, B и C
- Координаты точек N и M
- Длину медиан AN и BM

Опишите шаги для нахождения каждой из этих величин и приступайте к решению!