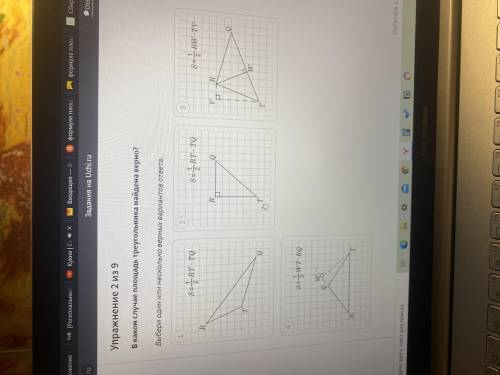
В каком случае площадь треугольника найдена верно?

4

Объяснение:

На 1 рисунке изображён тупоугольный треугольник.

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

RT и TQ - стороны ΔRTQ.

⇒ площадь данного треугольника найдена неверно.

На 2 рисунке изображён прямоугольный треугольник.

Площадь прямоугольного треугольника равна половине произведения его катетов.

RT - катет ΔRTQ, а TQ - гипотенуза.

⇒ площадь данного треугольника найдена неверно.

На 3 рисунке изображён тупоугольный треугольник.

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

TV и RW - высоты ΔRTQ.

⇒ площадь данного треугольника найдена неверно.

На 4 рисунке изображён тупоугольный треугольник.

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

RW - сторона ΔRTQ, а TW - высота, проведённая к RW.

⇒ площадь данного треугольника найдена верно.

Чтобы ответить на этот вопрос, нужно рассмотреть все три варианта и проверить, найдена ли площадь треугольника верно в каждом из них.

1. Вариант А:
В данном варианте используется формула для нахождения площади треугольника, где известны длины двух сторон и угол между ними.
Длина стороны AC равна 5, длина стороны AB равна 4 и угол между ними равен 60 градусов.
Для расчета площади треугольника по этой формуле нужно умножить половину произведения длин сторон на синус угла между ними:
Площадь = 0.5 * 4 * 5 * sin(60) ≈ 0.5 * 20 * 0.87 ≈ 8.66
В данном варианте площадь треугольника найдена верно.

2. Вариант Б:
В данном варианте используется формула для нахождения площади треугольника, где известны длины трех сторон.
Длина стороны AC равна 5, длина стороны BC равна 7 и длина стороны AB равна 4.
Для расчета площади треугольника по этой формуле нужно использовать полу-периметр треугольника (сумму длин всех сторон, разделенную на 2) и формулу Герона:
Полупериметр = (AB + BC + AC) / 2 = (4 + 7 + 5) / 2 = 16 / 2 = 8
Площадь = √(8 * (8-4) * (8-7) * (8-5)) = √(8 * 4 * 1 * 3) = √(96) ≈ 9.80
В данном варианте площадь треугольника найдена верно.

3. Вариант В:
В данном варианте используется формула для нахождения площади треугольника, где известны длина одной стороны и высота, проведенная к этой стороне.
Длина стороны BC равна 6, а высота, проведенная к этой стороне, равна 4.
Для расчета площади треугольника по этой формуле нужно умножить половину произведения длины стороны на высоту:
Площадь = 0.5 * 6 * 4 = 12
В данном варианте площадь треугольника найдена верно.

Таким образом, площадь треугольника найдена верно в каждом из представленных вариантов (А, Б и В).