ІВ, ХЕЛП МІ, ПЛІССС <333

Даны вектора а(2;-2;1) , b(8;4;1). Найти площадь треугольника, построенного на векторах 2а и b.

Объяснение:

S=1/2*a*b*sin(a;b),  где а и b  стороны треугольника.

Сторонами треугольника будут отрезки на которых лежат вектора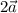 и .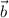

Найдем координаты вектора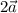  (2*2;-2*2;1*2 ) или  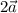 (4;-4;2 ).

Длина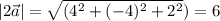

Длина /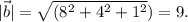

Найдем угол между ними по формуле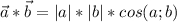

4*8-4*4+2*1=6*9*cosα ⇒ cosα=18/54 ,cosα=1/3.

По основному тригонометрическому тождеству

sinα=√(1-1/9)=(2√2)/3

( ед²)