Відрізок bm - медіана трикутника abc, відрізок de - середня лінія трикутника abm. чому дорівнює площа трикутника abc, якщо площа чотирикутника dbme дорівнює 12 см квадратних
Другие вопросы по теме Геометрия
Популярные вопросы
- Дед мазай плыл на лодке по течению реки зайцев. скорость течения реки 4 км/ч....
3 - Визначити ккд двигуна піднімального крана, який за 1 год піднімає на висоту 30...
2 - Ученик загадал число затем умножил его на 8 отнял 4 разделил на 6 умножил на...
3 - Улыбнись приятелю, с которым ты вчера повздорил. помирись с ним....
2 - Выпишите личные местоимения. мне, друг друга, нашего, некто, чего, себе, вас,...
3 - Напряжение на зажимах цепи u=100sin314t . каковы показания амперметра и вольтметра...
3 - Впрогрессии известно что в1=2 q=-2. найдите пятый член этой прогрессии...
3 - Соч по всемирной 4 четверть 7 класс...
1 - Лукашик иванова 780 сборник по ...
3 - Мы живем на огромной и в то же время хрупкой планете земля. диктант...
3
Поскольку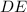 - средняя линия треугольника ABM, то
- средняя линия треугольника ABM, то 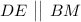 , тогда
, тогда 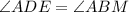 как соответственные углы при
как соответственные углы при 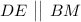 и секущей
и секущей 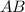 и
и  у треугольников
у треугольников 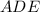 и
и 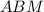 общий, следовательно,
общий, следовательно, 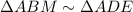 , коэффициент подобия
, коэффициент подобия 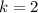
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Медиана разбивает треугольник на два треугольника одинаковой площади. То есть,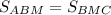 , следовательно,
, следовательно,
ответ: 32 см².