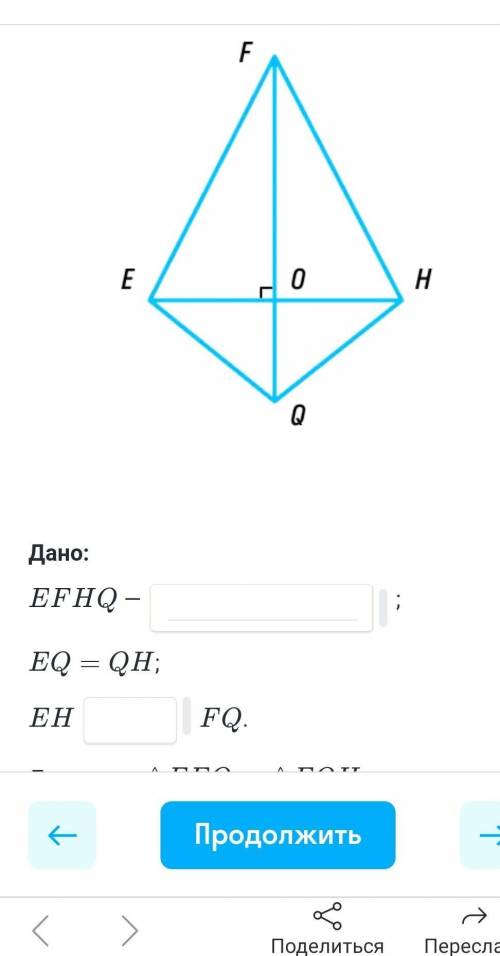
В четырехукгольнике EFHQ EQ=EH, EH пересекает FQ под прямым углом. Докажи что треугольник FEQ и FQH равны
Другие вопросы по теме Геометрия
Популярные вопросы
- Жарықта 0,6 моль хлор мен 15,68 л (к.ж) этанды араластырғанда түзілетін...
2 - -тапсырма Сұрақтарға жауап беріп, кестені толтырыңыз. № Сұрақ Жауап...
2 - Какие авторы в 19 веке и как отображали несправедливость ?...
3 - Так ли актуальна проблема сохранения природы, не слишком ли она преувеличена...
3 - ПРЕДМЕТ МИСТЕЦТВО Твір-роздум «Мистецтво – зв’язок минулого з майбутнім»...
3 - раз заливаю и пишут фсякую фегню то-есть 15...
1 - Степень какого одночлена равен 8...
3 - Берілген термин сөздерді пайдаланып, мәтін мазмұны бо.йынша сұрақ...
3 - Выпишите во местоимения и укажите их грамматические признаки. Белеет...
2 - В организме человека химические элементы разделяется на микро и макроэлементы...
2
Дано:
- EFHQ - четырехугольник
- EQ=EH
- EH пересекает FQ под прямым углом
Нам нужно доказать, что треугольники FEQ и FQH равны.
Доказательство:
Шаг 1: Рассмотрим треугольник EQH.
В этом треугольнике у нас есть две стороны, которые равны по условию: EQ=EH. Также у нас есть угол, пересекающий эти стороны под прямым углом. Следовательно, по определению прямоугольного треугольника EQH является прямоугольным.
Шаг 2: Посмотрим на треугольник FQH.
Мы знаем, что EH пересекает FQ под прямым углом. Это означает, что угол FQH тоже прямой. Таким образом, у нас есть два прямых угла в треугольнике FQH - FQH и EQH.
Шаг 3: Сравниваем треугольники.
У нас есть два прямоугольных треугольника - EQH и FQH. Оба треугольника имеют общую боковую сторону - EH. Это означает, что у них также есть общую гипотенузу - EH.
Таким образом, по теореме о гипотенузе(Leg-Leg Theorem) мы можем сказать, что треугольники FEQ и FQH равны, потому что они имеют две равные стороны - FE и FH, а также гипотенузу EQ.
Треугольники FEQ и FQH равны.
Это завершает доказательство.