ІВ, БУДУ ВДЯЧНА ЗА ДО !! ♡ (Известно, что |а| = 2, |б| = 3, |а + б| =√19. Вычислите: а) Угол между векторами а и б; б)

Question

Геометрия: ІВ, БУДУ ВДЯЧНА ЗА ДО !! ♡ (Известно, что |а| = 2, |б| = 3, |а + б| =√19. Вычислите: а) Угол между векторами а и б; б) |2а - б|)

дазз · Answer

Известно, что |а| = 2, |b| = 3, |а + b| =√19. Вычислите:

а) Угол между векторами а и b; б) |2а - b| .

Объяснение:

a)По правилу параллелограма суммой векторов a и b будет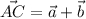 $\displaystyle \vec{AC}= \vec{a} + \vec{b}$ . Значит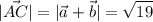 $\displaystyle |\vec{AC} | =| \vec{a} + \vec{b}|=\sqrt{19}$

Пусть α угол между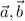 $\displaystyle \vec{a} , \vec{b}$ .Тогда ∠АВС=180°-α

ΔАВС, по т косинусов

АС²=АВ²+ВС²-2*АВ*ВС*cos(180-α)

19=4+9-2*2*3*(-cosα),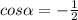 $cos\alpha =-\frac{1}{2}$ , α=120°

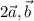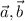б) Угол между векторами $\displaystyle 2 \vec{a} , \vec{b}$ равен 120° , тк эти вектора соноправлены с векторами $\displaystyle \vec{a} , \vec{b}$ .

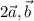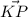Разностью векторов $\displaystyle 2 \vec{a} , \vec{b}$ будет $\displaystyle \vec{KP}$ Найдем его длину из ΔОРК по теореме косинусов КР²=ОР²+ОК²-2*ОР*ОК*cos∠РОК ,