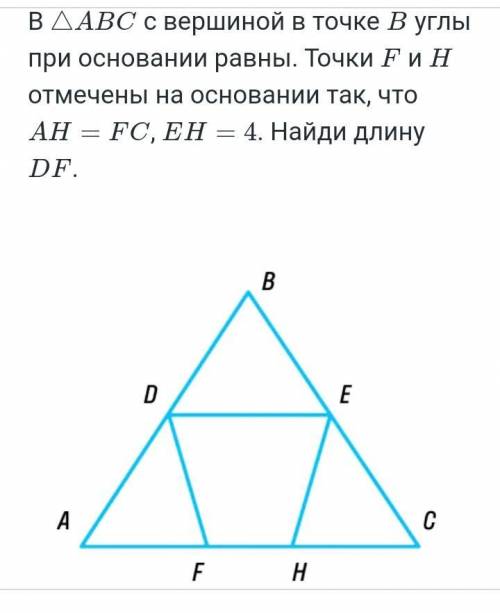
В авс с вершиной в точке в углы при основании равны. точки f и н отмечены на основании так, что ah= fc, eh= 4. найди длину df.
Другие вопросы по теме Геометрия
Популярные вопросы
- Скорость самолета равна 12 км/мин. Вырази его скорость в километрах в час....
1 - Самолет и вертолет летят в одном направлении. Скорость самолета 720 км/ч,...
3 - За минуту автомобиль проехал 2 км. Какое расстояние он проедет за час?...
3 - Щука плывет за карасем. Скорость щуки 10 м/с, а скорость карася 6 м/с....
1 - Старуха Шапокляк забыла в автобусе авоську и заметила это, когда автобус...
3 - Напиши числа от 1 до 10 с четырех четверок, вставляя между ними, если это...
3 - Чук и Гек вышли одновременно навстречу друг другу и встретились через 6...
1 - Пусть А — множество натуральных решений неравенства 5 ≤ x < 9, а В — множество...
1 - Волк гонится за зайцем. Скорость волка 14 м/с, а скорость зайца 10 м/с....
3 - Запиши 3 решения неравенства 7 < у < 8 сначала в виде смешанных чисел,...
1
CH = FC - FH
Так как AH = FC по условию, то AF = CH.
2) ∠DFA = 180° - ∠DFH, так как эти углы смежные,
∠EHC = 180° - ∠EHF, так как эти углы смежные.
Так как ∠DFH = ∠EHF по условию, то ∠DFA = ∠EHC.
3) Рассмотрим ΔADF и ΔCEH:
AF = CH (доказано в п. 1)
∠DFA = ∠EHC (доказано в п. 2)
∠DAF = ∠ECH по условию, значит
ΔADF = ΔCEH по стороне и двум прилежащим к ней углам.
В равных треугольниках против равных углов лежат равные стороны:
DF = EH = 4 см