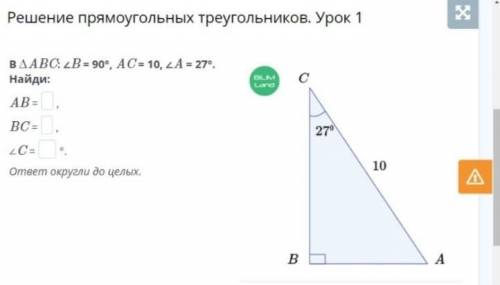
В ∆ABC: ∠B = 90°, AC = 10, ∠A = 27°. Найди: AB, BC, ∠C. ответ округли до целых.

Добрый день! Давайте рассмотрим данный треугольник ∆ABC и найдем все необходимые значения.

У нас есть следующие данные:
∠B = 90° (прямой угол)
AC = 10
∠A = 27°

Первое задание - найти сторону AB.

Для этого воспользуемся тригонометрической функцией синуса, так как у нас есть противолежащий ∠A катет и гипотенуза. Формула для нахождения стороны треугольника по теореме синусов:

AB/sin(∠A) = AC/sin(∠B)

Так как ∠B = 90°, то получаем:

AB/sin(∠A) = AC/sin(90°)

sin(90°) = 1, поэтому уравнение упрощается до:
AB/sin(∠A) = AC/1

Преобразуем уравнение, чтобы получить AB в одночлене:
AB = AC * sin(∠A)

Заменяем значения:
AB = 10 * sin(27°)
AB ≈ 4.65 (округляем до целого числа - 5)

Ответ: AB ≈ 5.

Второе задание - найти сторону BC.

Так как у нас есть прямой угол ∠B, то сторона BC будет являться гипотенузой треугольника ∆ABC. Значит, BC = AC = 10.

Ответ: BC = 10.

Третье задание - найти угол C.

Угол C является внутренним углом треугольника и можем найти, используя угловую сумму треугольника.

∠A + ∠B + ∠C = 180°

Заменяем известные значения:
27° + 90° + ∠C = 180°

Прибавляем известные значения:
117° + ∠C = 180°

Вычитаем 117°:
∠C = 180° - 117°
∠C = 63°

Ответ: ∠C = 63°.

Таким образом, мы нашли все значения, которые требовались в задаче:
AB ≈ 5
BC = 10
∠C = 63°.