Усеченный конус с радиусами оснований 3 и 5 и полный конус такой же высоты имеют равные объемы. Найти радиус основания полного конуса.

Ответы

alexandra44444 13.10.2020 20:03

7 см

Объяснение:

Формула объема усеченного конуса: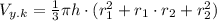 $V_{y.k} = \frac{1}{3} \pi h\cdot(r_{1}^{2} + r_{1}\cdot r_{2} + r_{2}^{2})$

Формула объема конуса: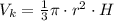 $V_{k} = \frac{1}{3} \pi \cdot r^{2} \cdot H$

Т.к. по условию объемы равны и высоты равны, то приравниваем соответствующие формулы:

$\frac{1}{3} \pi h\cdot(r_{1}^{2} + r_{1}\cdot r_{2} + r_{2}^{2}) = \frac{1}{3} \pi \cdot r^{2} \cdot h\\\\\\$

Т.к. высоты равны, то сокращаем обе части равенства на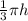 $\frac{1}{3}\pi h$ и получаем:

$r_{1}^{2} + r_{1}\cdot r_{2} + r_{2}^{2} = r^{2} \\\\3^{2} + 3\cdot 5 + 5^{2} = r^{2} \\\\9 + 15 + 25 = r^{2} \\\\r^{2} = 49\\\\r = \sqrt{49}$

r = 7 (см)

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

lakomkin2007 14.05.2020 08:49

maksymmakarec 14.05.2020 08:49

Отрезок Ak, где А (-2:1),В(3:2)...

Maksim777900 14.05.2020 08:49

karpovkonstanti 14.05.2020 08:48

aleks1yus 14.05.2020 08:48

Marina22111 14.05.2020 08:48

dias1101 14.05.2020 08:48

sergeygrachev 28.05.2019 10:20

Daniil199511 28.05.2019 10:10

slavakonst 28.05.2019 10:10

Усеченный конус с радиусами оснований 3 и 5 и полный конус такой же высоты имеют равные объемы. Найти радиус основания полного конуса.​