Усі бічні грані піраміди нахилені до основи під кутом 60 градусів. Зайдіть площу бічної поверхні піраміди, якщо її основа - трикутник зі сторонами 12 см, 39 см, і 45 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Как правильно написать слово грядки...
1 - Сочинение по рассказу в. г. распутина на тему . заранее...
3 - Как климат влияет на водное и рыбное хозяйство на территории беларуси...
1 - Решите велосипедист и пешеход одновременно отправились из деревни на озеро по одной...
2 - Хоть кто-нибудь, тему не поняла, а уже контрольная.. 1. на рисунке ав║сd.(трапеция...
3 - Какие вопросы можно придумать для произвидения остров м.пришвина?...
2 - Определи падеж имен существительных в тексте прежде чем поставить цветы в вазу...
3 - Зредагуйте словосполучення введіть їх у речення. слідуюча зупинка, розглянули наступні...
3 - Катер расстояние между пунктами a и b со скоростью 65 км/ч за 3 ч. за сколько времени...
1 - Достижения японии. например: войны или чтото другое...
3
Нехай є трикутна піраміда, сторони основи якої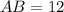 см,
см, 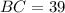 см,
см, 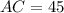 см. Якщо всі бічні грані піраміди нахилені до основи під кутом
см. Якщо всі бічні грані піраміди нахилені до основи під кутом 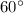 , то висота
, то висота 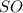 піраміди лежить у центрі
піраміди лежить у центрі 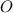 вписаного кола, де
вписаного кола, де 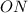 ,
, 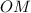 та
та 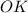 — радіуси цього кола.
— радіуси цього кола.
Треба знайти площу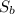 бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
Знайдемо площу основи за формулою Герона:
Знайдемо радіус вписаного кола:
Отже,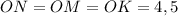 см.
см.
Розглянемо прямокутний трикутник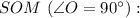
Розглянемо трикутник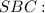
Розглянемо трикутник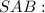
Розглянемо трикутник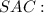
Отже, площею бічної поверхні заданої піраміди буде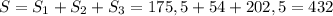 см².
см².
Відповідь: 432 см².