1. Геометрия
  2. Упрямокутній трапеції

Упрямокутній трапеції діагональ, проведена з вершини тупого кута, дорівнює бічній стороні. знайдіть відношення середньої лінії цієї трапеції до її більшої основи

SchoolZnatok SchoolZnatok    3   29.08.2019 11:46    2

Ответы
Манюня589 Манюня589  06.10.2020 02:49

Достроив до параллелограмма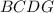 BCDG получим что 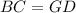BC=GD, но так как треугольник 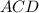ACD - равнобедренный, то 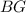BG - высота, медиана и биссектриса, следовательно,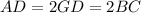 AD=2GD=2BC

Средняя линия трапеции равна полусумме оснований

FE=\dfrac{AD+BC}{2}=\dfrac{2BC+BC}{2}=\dfrac{3BC}{2}

Таким образом,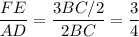 \dfrac{FE}{AD}=\dfrac{3BC/2}{2BC}=\dfrac{3}{4}

ответ: 3 : 4.


Упрямокутній трапеції діагональ, проведена з вершини тупого кута, дорівнює бічній стороні. знайдіть
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Milena0011 Milena0011  07.10.2019 14:20
Установите соответствие между треугольниками и радиусами описанной (r) и вписанной (r) окружностей этих треугольников...
Sultikutan Sultikutan  02.09.2019 02:00
Вравнобедренном треугольнике abc с основанием ac сумма углов a и c равна 156°. найдите углы треугольника abc. мерси)...
otepovaaazan otepovaaazan  02.09.2019 02:00
26 ! заранее ! 1. в прямоугольном треугольнике всегда два угла острых и один прямой. 2. в прямоугольном треугольнике всегда один острый угол, один прямой угол и один тупой угол. 3....
Tapoocek Tapoocek  08.04.2021 11:04
Бічна сторана рівнобeдриного трикутника ділиться точкою дотику вписаного кола у відношeні 2 :3 рухаючи від вeршини кута при основі трикутника Знайдить основу трикутника та його пeримeтр...
Новичок1532 Новичок1532  08.04.2021 11:06
Який кут утворюють вектори а(-2;1;3) і в(1:4;2)​...
ggwp49 ggwp49  05.05.2021 05:40
№1 На плоскости даны точки A (5; -2) и B (-7; 3). Найти длину отрезка AB по координатам концов №2 Если M (3; 1) и N (-1; 4), найти радиус и координаты центра окружности диаметром...
varfo varfo  31.08.2019 14:20
Дан равносторонний треугольник abc. найдите величину внешнего угла при вершине c....
arzumirzeyeva arzumirzeyeva  31.08.2019 14:20
(q_q) билет 1 1.понятие прямой и отрезка и взаимное расположение двух прямых. 2.первый признак равенства треугольника. билет 2 1.луч угол и виды углов. 2.второй признак равенства...
Anastasiagoodnastia Anastasiagoodnastia  04.05.2020 07:11
Найдите длину отрезка АВ.если А(2;-1) и В (1;3)...
IndiAkent IndiAkent  14.01.2021 13:21
Тестилеу кезеннинде орындалатын арекеттер информатика...

Популярные вопросы