Упростите выражение a) 1/cos2A -1
б) 1/sin²A -1
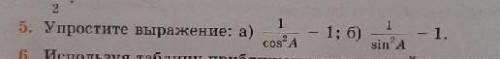
Другие вопросы по теме Геометрия
Популярные вопросы
- Составьте рассказ, используя ключевые слова. Ключевые слова: первые люди,...
2 - 7. У скільки раз зросте швидкість хімічної реакції CO + 3H2 = CH4 + H2O...
2 - «Астана – өнер ордасы ма?» деген тақырыпта келісу не келіспеу эссесін жазыңыз....
1 - 2.Определите тему текста 5 класс сор...
3 - СОР ПО ГЕОМЕТРИИ (Я НЕ СМОГ НАЙТИ ФОТКИ)ВОТ КОРОЧ ССЫЛКА ТАМ ЕСТЬ ОТВЕТЫ...
2 - БББПАААЛЛЛООО Етіс түрлеріне талдау жаса орнатылыпты салынған п отом создам...
3 - Обьясните написание ь в слове разольёшь?...
1 - не просто сам не смог:/ P.S это 6 класс...
2 - Обчисліть кількість речовин в порції води, що містить кількістю речовин...
3 - с казахским за качественный ответ ...
3
a) Нам нужно упростить выражение 1/cos2A - 1.
Для начала, давайте поймем, что такое cos2A. Косинус второй степени угла A будет обозначаться как cos²A, и он равен квадрату cosA.
Поэтому первый шаг, который мы сделаем, это заменим cos²A на (cosA)². Получаем следующее выражение: 1/(cosA)² - 1.
Далее, чтобы упростить дробь 1/(cosA)², нам нужно разложить дробь на две части. Общий знаменатель у нас уже есть, это (cosA)², поэтому первую часть дроби просто оставим без изменений, а вторую часть упростим: 1/(cosA)² = 1/(cosA * cosA) = 1/cosA * 1/cosA.
Заметим, что первая часть дроби равна 1/cosA, так как (cosA * cosA) = (cosA)². Теперь наше выражение будет выглядеть так: 1/cosA * 1/cosA - 1.
Сопоставляя с выражением из вопроса, получаем ответ: 1/cosA * 1/cosA - 1.
b) Теперь рассмотрим второе выражение 1/sin²A - 1.
Аналогично предыдущему случаю, разложим выражение на две части с общим знаменателем.
1/sin²A = 1/(sinA * sinA) = 1/sinA * 1/sinA.
Теперь наше выражение принимает вид: 1/sinA * 1/sinA - 1.
Сравнивая с изначальным выражением, получаем ответ: 1/sinA * 1/sinA - 1.
Надеюсь, данное объяснение помогло вам понять процесс упрощения данных выражений. Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать их!