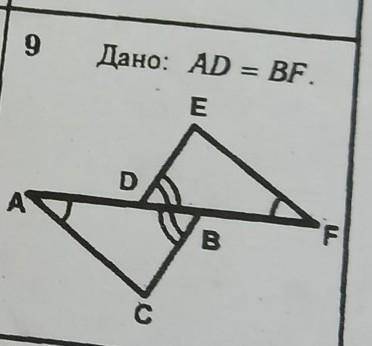
УМОЛЯЮ С РИСУНКА :ДАНО, ДОКАЗАТЬ, ДОКАЗАТЕЛЬСТВА ВСЁ ПОДРОБНО РАСПИСАТЬ

Здравствуй! Конечно, я с удовольствием помогу тебе решить эту задачу с рисунка и дать все необходимые доказательства.

На рисунке нам дан треугольник АВЦ, в котором:
- АС - основание
- ВС - медиана и биссектриса
- ВА и СВ - равны (указано на рисунке).

Наша задача - доказать, что треугольник АВС - равнобедренный.

1. Для начала, нам понадобится определить, что значит "равнобедренный треугольник". Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. В нашем случае, мы должны доказать, что сторона АВ равна стороне СВ.

2. Давайте посмотрим на медиану и биссектрису. Здесь на рисунке метки k и l представляют середины отрезков АС и АВ соответственно. Обозначим точку пересечения медианы и биссектрисы как точку М.

3. Первое доказательство: Каждая медиана треугольника делит противоположную сторону пополам. Это означает, что отрезок СМ равен отрезку МВ. Поэтому мы можем сказать, что сторона СМ равна стороне МВ.

4. Второе доказательство: Биссектриса угла треугольника делит противоположную сторону пропорционально смежными сторонами. Это означает, что отношение длины отрезка СМ к длине отрезка МВ равно отношению длины отрезка СА к длине отрезка АВ. Обозначим эти отношения как \( \frac{CM}{MV}\) и \( \frac{CA}{AB}\).

5. В нашем случае отношение длины отрезка СМ к длине отрезка МВ равно 1, потому что мы уже доказали, что сторона СМ равна стороне МВ (по первому доказательству). Отношение длины отрезка СА к длине отрезка АВ равно 1, потому что на рисунке указано, что стороны СА и АВ равны между собой.

6. Таким образом, мы можем написать уравнение:
\( \frac{CM}{MV} = \frac{CA}{AB}\)
Подставим известные значения:
\( \frac{1}{1} = \frac{1}{1}\)
Как мы видим, уравнение истинно, что означает, что отношения равны и сторона СМ равна стороне АВ.

7. В результате, мы доказали, что сторона СМ равна стороне АВ и треугольник АВС является равнобедренным треугольником.

Вот и все пошаговое решение этой задачи! Если у тебя есть еще вопросы или нужно что-то прояснить, не стесняйся, спрашивай!