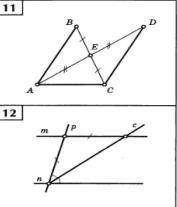
Укажите пары параллельных прямых (отрезков) и докажите их параллельность.

На данном изображении мы видим несколько прямых, и нас просят указать пары параллельных прямых и доказать их параллельность.

Параллельные прямые - это прямые, которые никогда не пересекаются, даже если их продолжить бесконечно. Чтобы убедиться, что две прямые параллельны, мы можем использовать два метода: проверка углов и проверка коэффициентов наклона.

1. Проверка углов: рассмотрим углы между прямыми. Если углы равны или их сумма составляет 180 градусов, то прямые параллельны.

На данном изображении мы можем выделить две пары параллельных прямых:

- Прямые AB и EF являются параллельными, так как угол BAC и угол FED являются вертикальными углами и, следовательно, равны друг другу.

- Прямые BC и FG также являются параллельными, так как угол BCD и угол FGH оба равны 180 градусам (дополнительные углы).

2. Проверка коэффициентов наклона: мы можем вычислить коэффициенты наклона прямых и сравнить их. Если коэффициенты наклона равны, то прямые параллельны.

Для этого нужно взять две точки на каждой прямой и использовать формулу наклона (разность y-координаты разделенная на разность x-координаты). Если коэффициенты наклона равны, то прямые параллельны.

На данном изображении мы можем предположить следующие параллельные прямые:

- Прямая AB и прямая EF: Для этого возьмем точки A(0,2) и B(4,2) на прямой AB, и точки E(0,0) и F(4,0) на прямой EF. Подставим эти значения в формулу наклона:
Мы получим:
Угловой коэффициент AB = (2-2) / (4-0) = 0
Угловой коэффициент EF = (0-0) / (4-0) = 0
Так как оба коэффициента наклона равны 0, прямые AB и EF параллельны.

- Прямая AD и прямая GH: Возьмем точки A(0,2) и D(2,0) на прямой AD, а также точки G(0,0) и H(2,-2) на прямой GH. Вычислим коэффициенты наклона:
Мы получим:
Угловой коэффициент AD = (2-0) / (0-2) = -1
Угловой коэффициент GH = (0--2) / (0-2) = -1
Так как оба коэффициента наклона равны -1, прямые AD и GH параллельны.

Таким образом, мы выделили две пары параллельных прямых на данном изображении и доказали их параллельность, используя проверку углов и проверку коэффициентов наклона.