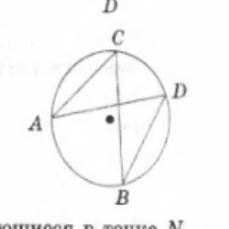
Укажите,какой из углов, изображенных на рисунке, является вписанным углом, опирающимся на одну дугу с углом :(

Угол ADB опирается на дугу AB, угол(вписанный) ACB так же опирается на дугу AB

На рисунке, у которого есть сектор и четыре угла, нам нужно определить, какой из углов является вписанным углом, опирающимся на одну дугу.

Вернёмся к определению вписанного угла. Вписанный угол - это угол, чей вершиной является точка на окружности, а его стороны - это хорды, начинающиеся в этой же точке и заканчивающиеся на окружности.

На рисунке мы видим две наибольшие окружности и две хорды, которые пересекаются внутри окружности. Углы, образующиеся при пересечении этих хорд, являются вписанными углами. Мы можем определить, какие углы являются вписанными, исследуя соответствующие хорды и углы.

Давайте рассмотрим каждую хорду по отдельности:

1. Хорда AC: Она проходит через центр окружности и делит ее на два равных сектора. Угол BAC, который расположен в одном из секторов, является вписанным углом. Поскольку углы A и C находятся в разных секторах и не опираются на эту хорду, они не являются вписанными углами.

2. Хорда BD: Она не проходит через центр окружности и не делит ее на два равных сектора. Углы BCD и BDA находятся в разных секторах и не опираются на эту хорду, поэтому они не являются вписанными углами.

3. Хорда CE: Она не проходит через центр окружности, но делит ее на два равных сектора. Угол CED, который расположен в одном из секторов, является вписанным углом. Угол CEB не опирается на эту хорду и не является вписанным углом.

Таким образом, вписанными углами, опирающимися на одну дугу, являются углы BAC и CED.

Окончательный ответ: Углы BAC и CED являются вписанными углами, опирающимися на одну дугу.