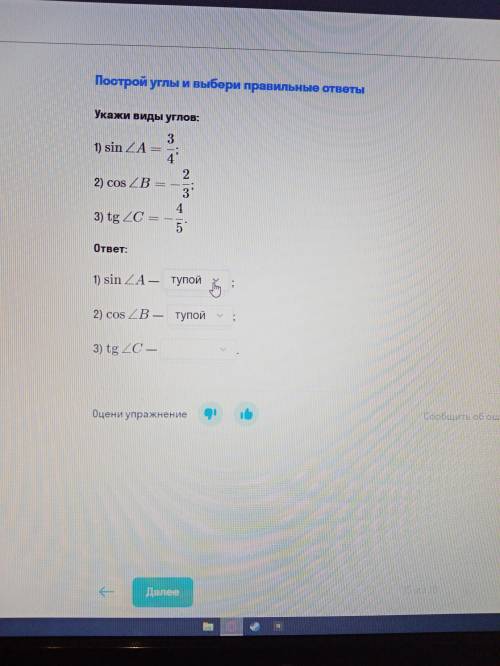
Укажи виды углов sin угла a =3 4

Для начала давайте разберемся, что такое синус угла. Синус угла - это тригонометрическая функция, которая определяется отношением противолежащего катета к гипотенузе в прямоугольном треугольнике.

Также мы знаем, что значение синуса угла лежит в интервале от -1 до 1.

Итак, у нас дано значение синуса угла a, которое равно 3/4. Нам нужно определить виды углов, соответствующих этому значению синуса.

Давайте найдем противолежащий катет и гипотенузу в прямоугольном треугольнике, построенном на угле a.

Мы можем воспользоваться теоремой Пифагора, которая утверждает, что квадрат гипотенузы равен сумме квадратов катетов:

гипотенуза² = противолежащий катет² + прилежащий катет²

из этого можно найти противолежащий катет:

противолежащий катет = √(гипотенуза² - прилежащий катет²)

Теперь давайте применим эту формулу. Пусть противолежащий катет равен 3, а гипотенуза равна 4. Тогда:

прилежащий катет² = гипотенуза² - противолежащий катет²
прилежащий катет² = 4² - 3²
прилежащий катет² = 16 - 9
прилежащий катет² = 7

Таким образом, прилежащий катет равен √7.

Теперь мы можем определить виды углов, соответствующие данному значению синуса угла a.

В нашем треугольнике, прямой угол равен 90 градусов, и угол a является острым углом. Когда синус угла положителен, как в нашем случае, это означает, что угол a находится в первом или втором квадранта, а не в третьем или четвертом.

Также мы знаем, что в прямоугольном треугольнике противолежащий катет относится к гипотенузе как синус угла:

sin a = противолежащий катет / гипотенуза

Таким образом, sin a = 3/4.

Мы уже вычислили значения противолежащего и прилежащего катетов, но нам также нужно учесть, что угол a является остроугольным углом.

Итак, мы можем сделать следующие выводы:

1. Угол a является остроугольным углом, так как его значение синуса положительное.
2. Противолежащий катет равен 3.
3. Прилежащий катет равен √7.
4. Гипотенуза равна 4.

Таким образом, у нас есть прямоугольный треугольник, в котором угол a является острым углом, и соответствующие значения катетов и гипотенузы.

Важно помнить, что все эти рассуждения основаны на предположении, что угол a является острым углом и что синус угла показывает отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.