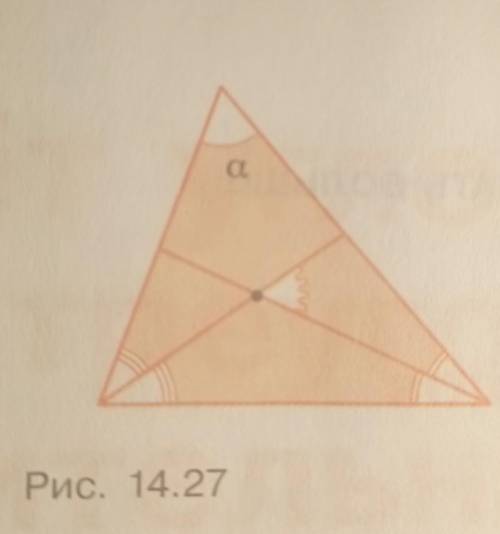
Угол треугольника равен a. Найдите угол между
биссектрисами двух других его
углов
(рис. 14.27).
​

Добрый день! Давайте разберем эту задачу.

У нас есть треугольник, у которого один из углов равен "а". И нас просят найти угол между биссектрисами двух других углов треугольника.

Чтобы решить эту задачу, нам придется использовать знания о свойствах углов треугольника, а именно свойства биссектрис.

Основная идея в решении задачи заключается в том, что биссектриса угла делит этот угол на две равные части. То есть, если мы проведем биссектрису угла "а", она разделит его на два угла, и каждый из этих углов будет равен "а/2".

Теперь нам нужно найти угол между биссектрисами двух других углов. Давайте обозначим этот угол как "b".

Поскольку мы знаем, что биссектриса делит угол на две равные части, у нас будет два угла в треугольнике, каждый из которых равен "b/2".

Теперь давайте рассмотрим треугольник, образованный этими двумя маленькими углами. В этом треугольнике сумма всех углов равна 180 градусов. Мы знаем, что сумма углов треугольника равна 180 градусов, поэтому можем записать следующее уравнение:

(b/2) + (b/2) + а = 180.

У нас уравнение с одной неизвестной, и мы можем его решить, чтобы найти значение угла "b".

Давайте сначала сложим "b/2" и "b/2", чтобы получить "b":

b + а = 180.

Теперь вычтем "а" из обеих частей уравнения:

b = 180 - а.

Итак, угол между биссектрисами двух других углов равен "180 - а".

Я надеюсь, что я был понятен и ответил на ваш вопрос. Если у вас все еще остались вопросы, пожалуйста, задавайте их.