Угол треугольника равен a. Найдите угол между биссектрисой его второго угла и биссектрисой внешнего угла при третьей вершине геометрия

Задание на фото. ​

Добрый день! Разберем задачу по порядку.

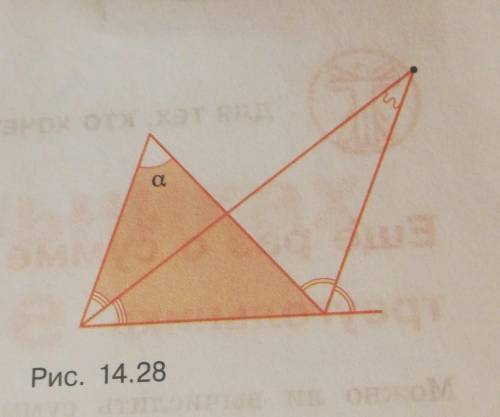
Изображение на фото показывает треугольник ABC, где угол ABC равен a. Требуется найти угол между биссектрисой угла B и биссектрисой внешнего угла ACB.

Для начала давайте вспомним определения биссектрис и свойства треугольников:

1. Биссектриса угла - это линия, которая делит данный угол на две равные части.

2. В треугольнике сумма всех углов равна 180 градусов.

Теперь перейдем к решению задачи.

У нас есть треугольник ABC, в котором угол ABC равен a. Давайте разделим угол ABC пополам с помощью биссектрисы. Обозначим точку деления биссектрисы как D. Из определения биссектрисы, мы знаем, что угол ABD и угол DBC равны между собой и равны a/2 каждый.

Теперь посмотрим на внешний угол ACB. Внешний угол образуется продолжением одной из сторон треугольника, в данном случае это сторона BC. Обозначим точку пересечения биссектры с продолжением стороны BC как E.

Свойство внешних углов треугольника говорит нам, что внешний угол равен сумме двух внутренних углов, не смежных с ним. В нашем случае это угол A и угол B, то есть угол ACB равен a + a/2.

Теперь у нас есть значения угла ACB и угла ABD. Для нахождения угла между биссектрисой угла B и биссектрисой внешнего угла ACB, нам нужно вычесть угол ABD из угла ACB: (a + a/2) - (a/2) = a.

Таким образом, угол между биссектрисой угла B и биссектрисой внешнего угла ACB равен a градусов.

Надеюсь, это решение понятно для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!