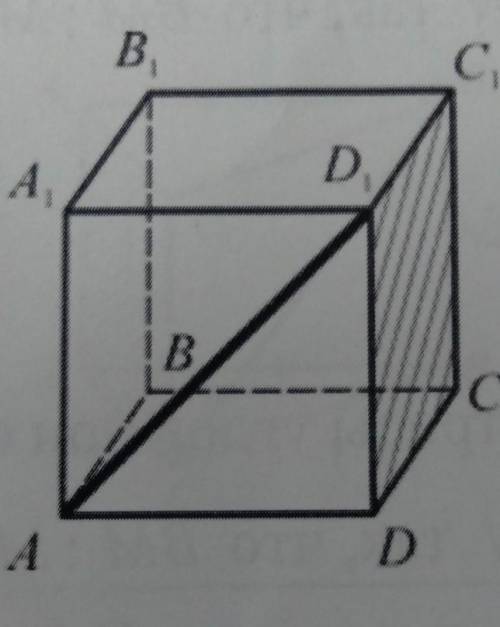
Угол между прямой и плоскостью 1 дано: abcda1b1c1d1-куб. найдите угол(ad1,(dd1c1))
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. каким характером обладал федор по мнению его современников? 2....
2 - Относится к местоимения слова нам тобой...
3 - Go carol singing скажите что это за выразительное средство? заранее...
3 - Ширина прямоугольника 4м, что составляет 6/7 длины. какова площадь...
1 - Переведи предложения и напиши что ты сделал вчера и успел сделать...
3 - Укажіть усі цілі від ємні числа, що більші за число -4,2 а) -3; -2;...
1 - Как дила миня завут это сикрет ты не узнаешь ну ты жи не манеяк карочи...
1 - Укажите предложения, в которых знаки препинания расставлены верно....
1 - Как разрезать прямоугольник длина которого 16 см а ширина 9 см на...
2 - Ширина прямоугольника равна 2 дм, а длина 5дм найди его площадь и...
1
На рисунке дан куб ABCDA1B1C1D1, и нам нужно найти угол между прямой AD1 и плоскостью (DD1C1).
Перед тем, как мы начнем решение, давай уточним некоторые вещи. Угол между прямой и плоскостью определяется как угол между нормалями (перпендикулярами) к этим геометрическим объектам. Также, нормаль к плоскости можно получить с помощью векторного произведения векторов, лежащих в этой плоскости.
Итак, первым шагом нам нужно найти нормаль (перпендикуляр) к плоскости (DD1C1). Для этого воспользуемся векторным произведением двух векторов, лежащих в этой плоскости.
Вектор, параллельный плоскости (DD1C1), можно получить, вычитая координаты точек D1 и D. Получим вектор D1D, который равен (-1 - 1, 1 - 1, 1 - 0) = (-2, 0, 1).
Теперь посмотрим на вектор DD1 и вектор DC1. Вектор DD1 можно получить, вычитая координаты точек D1 и D: DD1 = (-1 - 0, 1 - 0, 1 - 1) = (-1, 1, 0). Вектор DC1 можно получить, вычитая координаты точек C1 и C: DC1 = (1 - 0, 1 - 1, 1 - 1) = (1, 0, 0).
Теперь найдем векторное произведение векторов DD1 и DC1:
N = DD1 x DC1,
где N - нормаль (перпендикуляр) к плоскости (DD1C1).
Вычислим векторное произведение:
N = (-1, 1, 0) x (1, 0, 0).
Пользуясь правилом вычисления векторного произведения для векторов i, j, k, получим:
N = (0*i - 0*j, -1*i - 1*k, 1*j - 0*k) = (0, -i - k, j) = (0, -1, 0).
Теперь у нас есть нормаль N, которая перпендикулярна плоскости (DD1C1).
Далее, нам нужно найти нормаль (перпендикуляр) к прямой AD1. Но сначала найдем вектор AD1. Вектор AD1 можно получить, вычитая координаты точек D1 и A: AD1 = (-1 - 1, 1 - 1, 1 - 0) = (-2, 0, 1).
Теперь у нас есть вектор AD1. Заметим, что он также является направляющим вектором прямой AD1.
Теперь для нахождения нормали (перпендикуляра) к прямой AD1, мы можем использовать вектор AD1.
Таким образом, нормаль N к плоскости (DD1C1) и направляющий вектор AD1 прямой AD1 образуют угол. Мы можем найти этот угол с помощью скалярного произведения этих векторов:
cos(угол) = (N • AD1) / (|N| • |AD1|),
где (N • AD1) - скалярное произведение векторов N и AD1,
|N| - длина вектора N,
|AD1| - длина вектора AD1.
Вычислим скалярное произведение N и AD1:
N • AD1 = (0, -1, 0) • (-2, 0, 1) = 0*(-2) + (-1)*0 + 0*1 = 0.
Теперь найдем длину векторов N и AD1:
|N| = √(0^2 + (-1)^2 + 0^2) = √(1) = 1,
|AD1| = √((-2)^2 + 0^2 + 1^2) = √(4 + 0 + 1) = √(5).
Теперь, подставим значения в формулу для cos(угол):
cos(угол) = 0 / (1 • √(5)) = 0.
Таким образом, косинус угла между прямой AD1 и плоскостью (DD1C1) равен 0.
Теперь, чтобы найти сам угол, возьмем обратный косинус этого значения:
угол = arccos(0) = 90 градусов.
Итак, угол между прямой AD1 и плоскостью (DD1C1) равен 90 градусов.
Надеюсь, я смог объяснить эту задачу достаточно подробно и обстоятельно. Если у тебя остались вопросы, не стесняйся задавать их!