У трикутнику ABC кут C=40 градусів, кут A=80 градусів. Знайдіть кут між висотою AH і бісектрисою AK
Другие вопросы по теме Геометрия
Популярные вопросы
- Что означает понятия казённых во фразе белые дворы и слободы,...
2 - Укажите варианты ответов, в которых во всех словах одного ряда...
3 - Рассчитать общее сопротивление смешанного соединения R1234...
3 - из 4 деревянных досок длиной 150 см шириной 90 см и толщиной...
3 - в равнобедренном треугольнике ABC проведена высота к основанию...
2 - Написать заявление от своего лица на имя директора школы о предоставлении...
2 - Відображення історичних подій та козацтва у повісті Миколи Гоголя...
2 - Present Continuous or “to be going to”? (Поставьте глагол в соответствующую...
1 - только РАССТАВИТЬ только глаголы продолжать историю не нужно...
2 - Железный провод имеет длину 134 м. Как будет отличаться сопротивление...
2
Объяснение:
Угол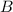 треугольника равен
треугольника равен
тогда в прямоугольном треугольнике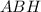
Но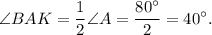
Значит